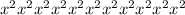
1) tg x + 3/tg x = 4, ОДЗ tg x <> 0
множим уравнение на tg(x), который по ОДЗ не ноль
(tg x)^2 - 4 tg x + 3 = 0
видим здесь квадратное уравнение относительно tg x.
а ещё видим, что сумма показателей степеней равна 1-4+3 = 0, поэтому один корень =1, второй по т.Виетта =3
уравнение распадается на совокупность
tg x = 1
tg x = 3
выписываем решение:
x = arctg(1) + pi n, где ncZ
x = arctg(3) + pi k, где kcZ
ну можно ещё вспомнить, что arctg(1) = pi/4
2) вспоминаем формулу косинуса двойного угла:
cos 2a = 2 cos^2 a - 1
если a = x/2, то исходное уравнение может быть представлено как
cos x + 1 + sin x = 0
вобщем, тут уже очевидно, что либо cos x =0, sin x =-1, либо cos x=-1, sin x =0
но чтобы совсем честно решать, придётся поколдовать.
синус направо и всё в квадрат!
(cos x +1)^2 = sin^2 x
cos^2 x + 2 cos x + 1 = 1 - cos^2 x
2 cos^2 x + 2 cos x = 0
cos x (cos x + 1) = 0
произведение обращается в ноль если хотя бы один из множителей обращается в ноль. значит опять совокупность:
cos x = 0
cos x = -1
x = pi/2 + pi n , ncZ,
x = pi + 2pi k, kcZ
но тут небольшая грабля. чуть выше мы возводили к вадрат. а нулевому косинусу соответствуют два значения синуса: +1 и -1. и один из них нам не подходит.
вобщем, проверяем корни и убеждемся, что из первой последователности половина значений выпадает (pi/2 + 2pi n НЕ являются корями. а pi/2 + pi + 2pi n - удовлетворяют)
ответ
x = 3pi/2 + 2pi n , ncZ,
x = pi + 2pi k, kcZ
38 см
Объяснение:
Пусть х см - одна из сторон прямоугольника, тогда (х + 5) см - другая сторона. Площадь прямоугольника равна 84 см².
Площадь находится по формуле S = ab, где a,b - стороны прямоугольника
х * (х + 5) = 84
х² + 5х = 84
х² + 5х - 84 = 0
D = 5² - 4 * 1 * (-84) = 25 + 336 = 361 = 19²
x₁ = (-5 - 19) / 2 = -24 / 2 = -12 ⇒ сторона не может быть отрицательна
x₂ = (-5 + 19) / 2 = 14 / 2 = 7
7 см - ширина прямоугольника
7 + 5 = 12 см - длина прямоугольника
Периметр находится по формуле P = 2 * (a + b), где a,b - стороны прямоугольника
2 * (7 + 12) = 2 * 19 = 38 см