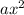 +x-3=0 больше 2-ух, а второй меньший двух объяснить решение, поскольку пытаюсь разобраться в теме.
+x-3=0 больше 2-ух, а второй меньший двух объяснить решение, поскольку пытаюсь разобраться в теме.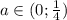
Объяснение:
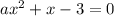
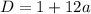
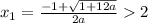
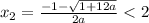
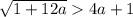
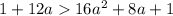
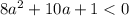
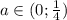
Давайте решение уравнения -9(8 - 9x) = 4x + 5 начнем с того, что откроем скобки.
Для этого применим дистрибутивный закон умножения:
-9 * 8 - 9 * (-9x) = 4x + 5;
-72 + 81x = 4x + 5;
Далее мы собираем в разных частях уравнения слагаемые с переменными и без.
81x - 4x = 5 + 72;
Приводим подобные в обеих частях полученного равенства:
x(81 - 4) = 77;
77x = 77;
Ищем неизвестный множитель:
x = 77 : 77;
x = 1.
Проверим верно ли мы нашли корень:
-9(8 - 9 * 1) = 4 * 1 + 5;
-9 * (-1) = 4 + 5;
9 = 9.
ответ: x = 1.
Объяснение:
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
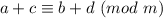
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
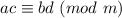
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
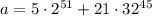
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 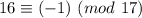 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 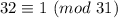 , получаем
, получаем
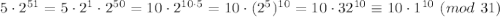
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
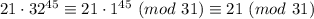
Остаток 21, чудесно. Выполняем последний шаг.
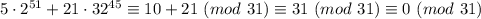
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
ответ: a∈( 0; 1/4)
Объяснение:
ax^2+x-3 = 0
Обязательное условие: уравнение имеет 2 корня
D=1+12a>0 → a > -1/12
a = 0 нам так же не подходит, ибо данное уравнение становится линейным.
Таким образом: a∈(-1/12;0) ∪ ( 0; ∞)
По условию ясно, что число 2 лежит между корнями параболы.
Из графических представлений ясно, что при a>0 между корнями лежит отрицательная часть параболы f(x) = ax^2+x-3, а при a<0 между корнями лежит положительная часть параболы. Данное условие эквивалентно следующему неравенству:
a*f(2)< 0
a(4a-1) < 0
a∈(0; 1/4)
Пересекая с условием: a∈(-1/12;0) ∪ ( 0; ∞), получаем ответ:
a∈(0; 1/4)