
a) 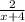
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
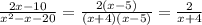
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
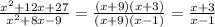
а) 2х-10/х^2-х-20=2(х-5)/(х-5)×(х+4)=2/х+4
х^2-х-20=0
D=b^2-4ac(D-дискриминант)
D=1^2-4×1×(-20)=1+80=81>0(2различных действительных корня)
Х1, 2=-b+-корень из D/2a
X1=-(-1)+9/2×1=1+9/2=10/2=5
X2=-(1)-9/2×1=1-9/2=-8/2=-4
Т.Е.Х1=5
Х2=-4
След.(х-5)×(х+4).
Подставляем в начало
Объяснение:
б) х^2+12х+27/х^2+8х-9=(х+3)(х+9)/(х-1)(х+9)=х+3/х-1
Записываем первое уравнение и приравниваем к 0
х^2+12х+27=0
D=b^2-4ac
D=(12)^2-4×1×27=144-108=36>0(2 различных действительных корня)
Х1, 2=-b+-корень из D/2a
X1=-12+6/2×1=-6/2=-3
X2=-12-6/2=-18/2=-9
Т.Е.Х1=-3
Х2=-9
След.(х+3)×(х+9)
Подставляем полученное выражение в числитель
Затем берём второе уравнение и приравниваем его к 0
х^2+8х-9=0
D=b^2-4ac
D=(8)^2-4×1×(-9)=64+36=100>0(2 различных действительных корня)
Х1, 2=-b+-корень изD/2a
X1=-8+10/2×1=2/2=1
X2=-8-10/2×1=-18/2=-9
Т.Е.Х1=1
Х2=-9
След.(х-1)×(х+9)
Подставляем полученное выражение в знаменатель
В решении.
Объяснение:
Формулы:
(а + в)³ = а³ + 3а²в + 3ав² + в³; куб суммы;
(а - в)³ = а³ - 3а²в + 3ав² - в³; куб разности.
а) (х + 2)³ = куб суммы =
= х³ + 3х²*2 + 3х*2² + 2³
= х³ + 6х² + 12х + 8;
б) (3 - х)³ = куб разности +
= 3³ - 3*3²*х + 3*3*х² - х³ =
= 27 - 27х + 9х² - х³;
в) (2a - b)³ = куб разности =
= (2a)³ - 3*(2a)²*b + 3*2a*b² - b³ =
= 8a³ - 12a²b + 6ab² - b³;
г) (3a + 2b)³ = куб суммы =
= (3a)³ + 3*(3a)²*2b + 3*3a*(2b)² + (2b)³ =
= 27a³ + 54a²b + 36ab² + 8b³.