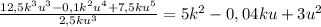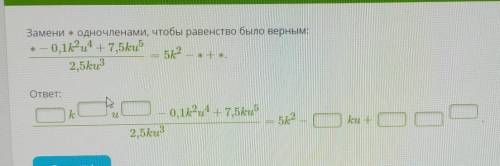
Найдем сначала точки пересечения линий второго порядка
Приравняем правые части уравнений
y =1/(x^2+1) y=x^2/2
1/(1+x^2)=x^2/2
Так как 1+x^2 не равно нулю умножим обе части уравнения на 2(1+x^2)
2 =(1+x^2)*x^2
х^4+x^2-2 =0
Сделаем замену переменных z=x^2
z^2+z-2=0
D =1+8=9
z1=(-1-3)/2=-2 (ответ не подходит так как x^2>0)
z2 =(-1+3)/2=1
x^2=1 x1=-1 x2=1
Получили два предела интегрирования от -1 до 1
интеграл I от -1 до 1I (1/(x^2+1)-(1/2)x^2)dx =(arctgx-(1/6)x^3 Iот -1 до1I=
= arctg(1)-1/6 -(arctg(-1)-(-1)^3/6) = пи/4-1/6+пи/4 -1/6 =пи/2=1,57
S=П/2~1,57
Решение
1)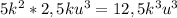
2)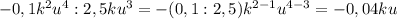
3)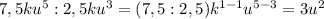
ответ: