Первый геометрический смысл производной)
Производная в точке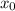 
равна угловому коэффициенту касательной к графику функции 
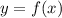в этой точке.
Пусть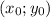 
- точка касания двух графиков. Тогда
y = -2x + 2 - касательная к графику y = -x² + p ⇒ k = -2
Производная функции: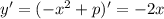 
Используя геометрический смысл производной, мы получим
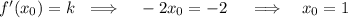
Получили абсциссу точку касания, тогда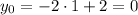 
Тогда, подставив точку (1;0) в первый график уравнения, найдем р
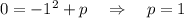
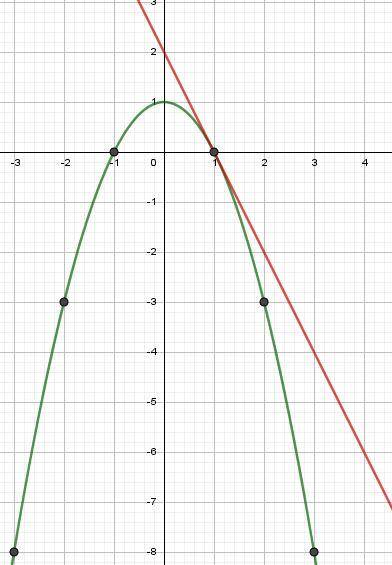
При р = 1 имеется общая точка (1;0) графика функции y = -x² + 1 и прямой y = -2x + 2.
y = -x² + 1 - парабола, ветви которой направлены вниз. Вершина параболы (0;1). Точки построения изображены на картинке.
y = -2x + 2 - прямая, проходящая через точки (0;2), (1;0).
Второй Определение через дискриминант)
Приравниваем функции: -x² + p = -2x + 2 или -x² + 2x + p - 2 = 0
D = b² - 4ac = 4 + 4(p-2) = 4(1 + p -2) = 4(p-1)
Чтобы графики имели одну общую точку, достаточно чтобы квадратное уравнение имело одно единственное решение, т.е. когда D = 0.
4(p-1) = 0
p = 1.
При р = 1, получим -x² + 2x + 1 - 2 = 0 ⇔ -(x-1)² = 0 ⇒ x=1
y = -1² + 1 = 0
Координаты точки касания двух графиков (1;0).
- log2_(2x+1) = - 2;
log2_(2x+1) = 2;
2x+ 1= 2^2;
2x = 3;
x= 1,5.
3)log2_(4 - 2x) + log2_3 = 1;
log2_((4-2x)*3 = 1;
log2_(12 - 6x) = 1;
12 - 6x = 2^1;
12 - 6x = 2;
- 6x = -10;
x = 10/6= 5/3.
4) log7_(x-1) = log7_2 + log7_3;
log7_(x-1) = log7_(2*3);
x - 1 = 6;
x = 7.
5)1 ≤ 7x - 3 < 49; +3
1 + 3 ≤ 7x < 49 + 3;
4 ≤ 7x < 52;
4/7 ≤ x < 52/7.
6) log2_(1 - 2x) < 0;
log2_(1 - 2x) < log2_1;
2 > 1; ⇒ 1 - 2x < 1;
- 2x < 1 - 1;
- 2x < 0; /-2 < 0;
x > 0
7) lg(0,5 x - 4) < 2;
lg(0,5x - 4) <lg100;
0,5x - 4 < 100;
0,5 x < 104; * 2>0;
x < 208
8) log0,2_(2x+3) ≥ - 3; 0,2 = 1/5 = 5^(-1);
- log5_(2x + 3) ≥ - 3; /-1 <0;
log5_(2x + 3) ≤ 3;
log5_(2x+3) ≤ log5_125;
5 > 1; ⇒ 2x + 3 ≤ 125;
2 x ≤ 122;
x ≤ 61.
В первом задании не понятно условие.