1. Числа A, B, C составляют геометрическую прогрессию;
2. Известны их произведение: A * B * C = 64;
3. Среднее арифметическое этих чисел: (A + B + C) / 3 = 14/3;
4. Основное уравнение:
B² = A * C = 64 / B;
B³ = 64;
B = 4;
5. Сумма трех чисел:
A + B + C = 14;
B / q + B + B * q = 14;
B * (1/q + 1 + q) = 4 * (1/q + 1 + q) = 14;
q² + q + 1 = 3,5 * q;
q² - 2,5 * q + 1 = 0;
q1,2 = 1,25 +- sqrt(1,25² - 1) = 1,25 +- 0,75;
6. q1 = 1,25 - 0,75 = 0,5;
A1 = B / q = 4 / 0,5 = 8;
C1 = B * q = 4 * 0,5 = 2;
7. q2 = 1,25 + 0,75 = 2;
A2 = B / q = 4 / 2 = 2;
C2 = B * q2 = 4 * 2 = 8.
ответ: так как не указано иное, считаем варианты равноценными: 2, 4, 8.
Объяснение:
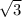 / 2 ( отмечаем эти точки )
/ 2 ( отмечаем эти точки )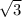 / 2 ( отмечаем эти точки )
/ 2 ( отмечаем эти точки )
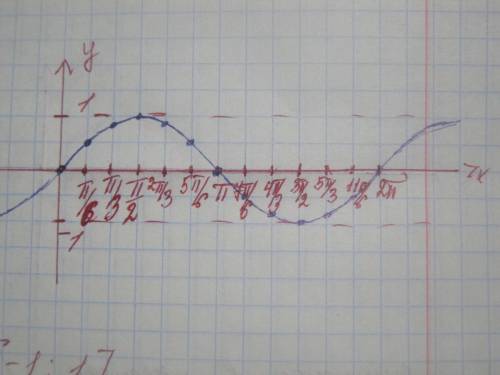
1. 8p-(6p^2+16p-15p-40)=8p-6p^2-p+40=7p-6p^2+40
2. 4x^2-8x+10x-20+20=4x^2+2x=2x(2x+1)
3. x^2-3x+5x-15-x^2-x=x-15
4.a^2-3a+a^2+a+4a+4=2a^2+2a+4