sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(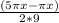
)cos(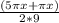
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
См. Объяснение
Объяснение:
№ 1
Задание
В прямоугольном треугольнике tgα=4. Найдите: sinα, cosα, ctgα.
Решение
1) tg²α = 1/cos²α - 1
4² = 1/cos²α - 1
1/cos²α - 1 = 16
(1-cos²α)/cos²α =16
16cos²α = 1-cos²α
17cos²α = 1
cos²α = 1/17
cosα = √(1/17) = √17/17 ≈ 0,2425356
2) tgα = sinα/cosα
sinα/cosα = 4
sinα/√17/17= 4
sinα = 4 · √17/17 = (4√17)/17 ≈ 0,9701425
3) ctg α = 1/tgα = 1/4 = 0,25
sinα = 4√17)/17 ≈ 0,9701425;
cosα = √17/17 ≈ 0,2425356;
ctgα = 0,25.
№ 2
Вычислить:
ctg240° + tg300° - sin(-225°) - cos495°.
Решение
1) ctg240° = ctg (180°+60°) = ctg60° = √3/3
2) tg300° = tg(270°+ 30°) = - сtg30° = - √3
3) - sin(-225°) = sin(225°) = sin(180° + 45°) = - sin45° = - √2/2
4) - cos 495° = - cos (360° + 135°) = - cos (135°) = - cos (180°- 45°) = cos 45° = √2/2
ctg240° + tg300° - sin(-225°) - cos495° = √3/3 - √3 - 2/2 +√2/2 =
= √3/3 - √3 ≈ - 1,1547
ответ: √3/3 - √3 ≈ - 1,1547