1. Вынесите общий множитель за скобку: а) 2 + 3 б) 83 + 122
2. Преобразуйте в многочлен, используя формулы
сокращенного умножения: а) ( − 3)2 ;
б) ( + 2)2 ; в) ( − 2)( + 2)
3. Разложите на множители: а) 3 − (2)3;
б) (3)3 + (2)3
4. Вычислите с формул сокращенного
умножения: а) 822 б) 522 − 482
5. Разложите на множители:
а) (2 + 4) − ( + 2)
б) 2( − ) + −
6. Выделите полный квадрат: а) 2 + 6
б) 2 − 8 + 15
7. Преобразуйте в многочлен:
(2 − 3)2 − ( + 2)( − 2)
;
;
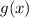и будет искомой фигурой.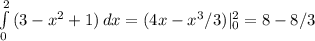
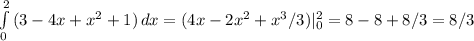
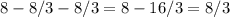(кв. ед.)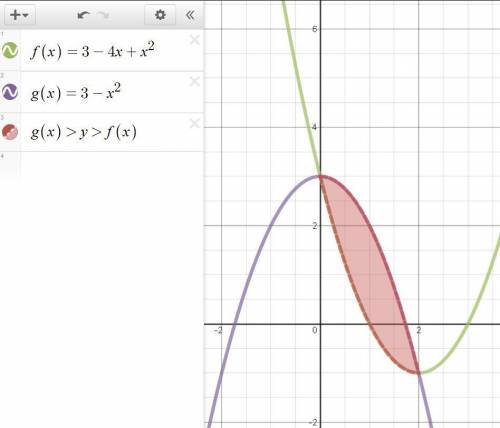
1)
2)
3)
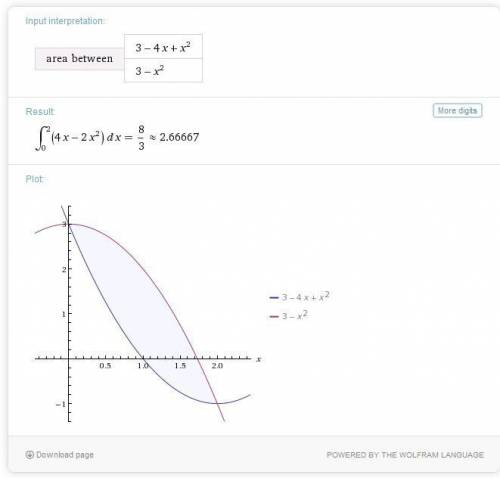
1) y=x²+10 - парабола , поднятая на 10 точек вверх, координаты вершины (0;10)
2) y=x²-5 - парабола, на 5 точек вниз, координаты вершины (0;-5)
3) y=(x+7)² - парабола, передвинутая на 7 точек влево, вершина (-7;0)
4) y=(x-8)²-парабола, передвинутая на 8 точек вправо, вершина (8;0)
4) y=x²
1) y=x²+5
2)y=x²-4
3)y=(x-3)²
4)y=(x+6)²
5)
На фото, c Ox пересекается график функции y=x²-4.
Точки пересечения с Ox (-2;0) и (2;0)
И y=x²-1
Точки пересечения с Ox (-1;0) и (1;0)
С Oy : y=x²-1, (0;-1)
y=x²+2,5 , (0;2,5)
y=x²-4, (0;-4)
y=x²+4,5, (0;4,5)