30% = 30/100 = 3/10
Пусть всего на трёх участках растёт х кустов малины, тогда на первом участке растёт (7/16)х кустов, на втором (3/10)х кустов, а на третьем (3/10)х - 9 кустов
Уравнение: х = (7/16)х + (3/10)х + (3/10)х - 9
х - (35/80)х - (24/80)х - (24/80)х = - 9
х - (83/80)х = - 9
(-3/80)х = - 9
х = - 9 : (-3/80)
х = 9 · 80/3
х = 3 · 80
х = 240
ответ: 240 кустов малины растёт на трёх участках.
Наш многочлен имеет вид
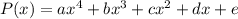
Пусть меньший его корень равен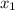 
. Так как корни образуют арифметичекую прогрессию, можем записать:
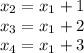
Многочлен раскладывается на линейный множители следующим образом:
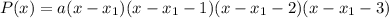
Напрашивается замена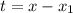 
. Тогда
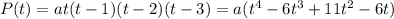
Нам нужно найти минимумы этой функции, поэтому дифференцируем:
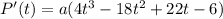
Теперь требуется найти корни этого многочлена. Используя теорему о рациональных корнях многочлена можно найти корень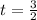 
Согласно теореме Безу,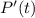 
должен делиться на 
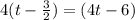. Разложим на множители, чтобы найти остальные корни:
![P'(t)=a(4t^3-6t^2-12t^2+18t+4t-6)=a[t^2(4t-6)-3t(4t-6)+(4t-6)]=a(4t-6)(t^2-3t+1)](/tpl/images/0952/7803/88744.png)
Решив квадратное уравнение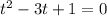 
, найдем корни
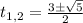
Расположив корни
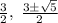
на числовой прямой и использовав метод интервалов, узнаем, что производная меняет знак с минуса на плюс в точках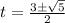 
, это и есть точки минимума. Переходя обратно к многочлену от x, получаем точки
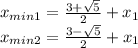
Квадрат расстояния между ними:
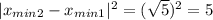
Часовая и минутная стрелки догоняют друг друга раз в 65 минут. Если они догоняют друг друга раз в 66 минут, то часы спешат на 1 минуту. Или же, если очень-очень точно считать, то, когда минутная проходит час от часовой, то проходит 60 минут, но минутная впереди на 5 минут. Когда минутная доходит до того 65-отрезка, то часовая еще 5/12 минут... и так очень долго будет продолжаться, пока геометрическая прогрессия не достигнет некоего предела. У меня получилось, что часы спешат на 6/11 минут, но вряд ли тут про это спрашивают). Хотя задача интересная.