1) a)y=3 б)x=3 в) (3;+∞) возрастает (-∞;3) убывает
2)а)у=-0,5 б) у=0,25 в) у=3
3) у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Объяснение:
1) находим по графику абсцисса -это х ордината это -у
2)подставляем вместо х значение и считаем
3) a)у(4)=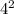 =16 б)у(-3)=
=16 б)у(-3)=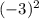 =9 в) у(2)=
=9 в) у(2)=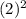 =4
=4
у(3)=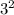 =9 у(-2)=
=9 у(-2)=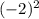 =4 у(-5)=
=4 у(-5)=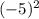 =25
=25
у(4)>y(3) y(-3)>y(-2) y(2)<y(-5)
Решение системы уравнений х=10
у=12
Объяснение:
Решить систему уравнений.Методом алгебраического сложения.
x/5-y/6=0
5x-4y=2
Нужно избавиться от дробного выражения в первом уравнении, общий знаменатель 30, надписываем над числителями дополнительные множители:
6*х-5*у=0
6х-5у=0
5х-4у=2
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, коэффициенты или при х, или при у были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают одно из уравнений, как бы подгоняют ко второму, можно умножать обе части уравнения на одно и то же число, делить.
Поэтому первое уравнение умножим на -5, а второе на 6:
-30х+25у=0
30х-24у=12
Складываем уравнения:
-30х+30х+25у-24у=12
у=12
Теперь подставляем значение у в любое из двух уравнений системы и вычисляем х:
5х-4*12=2
5х-48=2
5х=2+48
5х=50
х=10
Решение системы уравнений х=10
у=12
-36,6
Объяснение:
( х–3)²-12(х–3)+36=(9,3-3)²-12(9,3-3)+36=3-12(6,3)+36=3-75,6+36=-36,6