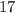и 
– среднеарифметическое равно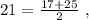 
и при этом 
на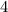 
меньше двадцати пяти и на 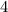больше семнадцати.
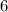монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на 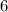монет меньше изначального, а у Пети на 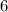монет больше изначального. А значит, вначале у Васи было на 
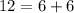монет больше, чем у Пети.
монет. Тогда у Пети 
монет.
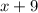монет, а у Пети-II будет 
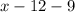монет. При этом у Пети-II монет в 
раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение:
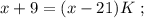
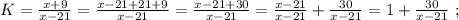
было целым, целой должен быть и результат деления в дроби, а чтобы было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 
откуда:
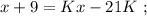
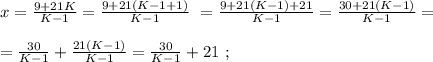
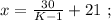
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет 
откуда: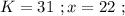
а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
Так как получилось разделить нацело, то 1234...9899 делится на 9.