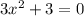
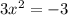
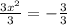
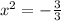
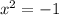
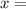 ±
±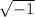
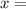 ±
±
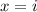

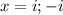
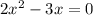
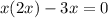
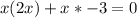
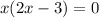
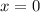
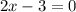
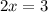
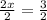
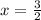
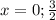
все таки математика настигла огромной волной и накрыла корнями и дробными степенями ???
(x)^1/n = ⁿ√x (например x^1/3 = ∛x x^1/2 = √x)
x² - y² = (x - y)(x + y)
(x + y)² = x² + 2xy + y²
(x^n)^m = x^(nn)
x^n * x^m = x^(n+m)
ⁿ√xⁿ = x (для положительных х)
x^-1 = 1/x
1. 64^1/6 = ⁶√(2⁶) = 2
2. 27 ^2/3 = ∛ 27² = ∛ (3³)² = 3² = 9
3. 0^51/4 = 0 (0 в любой положительной степени = 0)
5. x^1/2 = (x^1/4)²
(a^1/2 - b^1/2) / (a^1/4 + b^1/4) = (a^1/4 - b^1/4)(a^1/4 + b^1/4)/(a^1/4 + b^1/4) = a^1/4 - b^1/4
4. (x^1/3 + y^1/3)² - 2∛(xy) - 1/(∛y)^-2 = x^2/3 + 2x^1/3*y^1/3 + y^2/3 - 2x^1/3*y^1/3 - y^2/3 = x^2/3
^ - степень ( x^2/3 = ∛x² икс в степени две третьих)
Найдем сначала уравнение секущей:
Она проходит через две точки:х1=-1, у1 = 2*(-1)^2 = 2
и х2 = 2, у2 = 2*2^2 = 8
Ищем уравнение секущей в виде: y=kx+b
Подставим сюда две наши точки и решим систему, найдем k:
-k+b=2
2k+b=8 Вычтем из второго первое: 3k = 6, k= 2.
Наша искомая касательная должна быть параллельна секущей, значит имее такой же угловой коэффициент. k=2
Найдем точку касания, приравняв производную нашей ф-ии двум:
Y' = 4x = 2
x = 1/2
Уравнение касательной к ф-ии в т.х0:
у = у(х0) + y'(x0)(x-x0)
Унас х0 = 1/2, у(1/2) = 2*(1/4) = 1/2, y'(1/2)= 2.
Тогда получим:
у = 1/2 + 2(х - 1/2)
у = 2х -0,5 - искомое уравнение касательной.