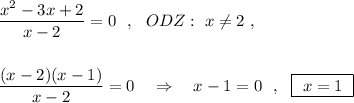
Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
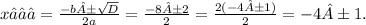
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
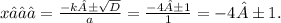
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
Объяснение:
сложение: просто складываешь сначала числа после запятой, затем перед запятой. проще всего столбиком (если ты только начинаешь учить это), НО чтобы целые числа были под целыми, а остаток под остатком (это на случай, если нужно будет складывать дроби 1,2 и 1, 25. над пятёркой в данном случае будет пусто, либо дописываешь ноль на это место).
умножение: опять же проще всего столбиком, но тут уже всё равно на местоположение запятой. не обращая внимание на запятую перемножаешь числа столбиком, а затем считаешь сколько в двух числах, которые ты умножал(а), цифр после запятой, и отсчитываешь столько же цифр с конца(!) полученного числа.
деление: делитель не может быть с остатком (в ручном подсчёте). если тебе нужно разделить 5,61 на 3,2 то нужно каждое из этих чисел умножить на десять (в уме), чтобы получилось 56,1 и 32. это делается для того, чтобы делитель был без остатка. если у дроби остаток больше (например 3,456) то нужно умножать будет уже не на 10, а на 1000.
вычитание работает так же как сложение, в нём так же как и в обычном вычитании столбиком можно занимать десяток у впереди стоящего числа