

Составить уравнение плоскости, проходящей через прямые (x−1)/3=(y+2)/2=(z−5(/(-2) и
⎪x=7+2t
⎨y=2−3t
⎪z=1+4t
Написать уравнение плоскости, проходящей через две заданные прямые можно, если эти прямые параллельны или пересекающиеся.
Нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки.
Уравнение первой прямой представим в параметрическом виде.
(x−1)/3=(y+2)/2=(z−5)/(−2) = a.
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
По непропорциональным коэффициентам параметров видно что прямые не параллельны.
Найдём точку пересечения прямых
x = 2t + 7,
y = -3t + 2,
z = 4t + 1,
и
x = 3a + 1,
y = 2a – 2,
z = -2a + 5.
Приравняем параметрические значения при одинаковых переменных.
2t + 7 = 3a + 1,
-3t + 2 = 2a – 2,
4t + 1 = -2a + 5.
=>
2t = 3a – 6,
-3t = 2a – 4,
4t = -2a + 4.
Приравняем правые части первого уравнения, умноженное на 2, и третье уравнение.
6a – 12 = -2a + 4,
8a = 16,
a = 16/8 = 2.
Подставим полученное значение а = 2 в параметрические уравнения второй прямой.
x = 3*2 + 1 = 7,
y = 2*2 – 2 = 2,
z = -2*2 + 5 = 1.
Найдём значение t по параметру а = 2.
2t = 3*2 – 6 = 0, t = 0,
-3t = 2*2 – 4 = 0, t = 0,
4t = -2*2 + 4 = 0, t = 0.
Подставим полученное значение t = 0 в параметрические уравнения первой прямой.
x = 2*0 + 7 = 7,
y = -3*0 + 2 = 2,
z = 4*0 + 1 = 1.
Значения перменных совпадают, значит, прямые пересекаются и найдена точка С их пересечения С(7; 2; 1).
Далее из уравнений прямых находим координаты не общих точек.
Из уравнения первой прямой (x−1)/3=(y+2)/2=(z−5)/(−2) определяем точку
А(1; -2; 5).
Найдём точку B на второй прямой, подставив t = 1.
x = 2*1 + 7 = 9,
y = -3*1 + 2 = -1,
z = 4*1 + 1 = 5.
Найдена точка В(9; -1; 5).
По трём точкам А(1; -2; 5), В(9; -1; 5), С(7; 2; 1).составляем уравнение плоскости.
Находим векторы АB и АC.
Вектор АВ = (9-1; -1-(-2); 5-5) = (8; 1; 0).
Вектор АC = (7-1; 2-(-2); 1-5) = (6; 4; -4).
Нормальный вектор плоскости АBC находим из векторного произведения векторов АB и АC.
i j k| i j
8 1 0| 8 1
6 4 -4| 6 4 = -4i + 0j + 32k + 32j - 0i - 6k =
= -4i + 32j + 26k.
Нормальный вектор плоскости АBC равен (-4; 32; 26).
Примем коллинеарный ему вектор с к = -2: (2; -16; -13)
Уравнение плоскости, проходящей через точку Mo(xo;yo;zo), с нормальным вектором n=(A;B;C) имеет вид A·(x–xo)+B·(y–yo)+C·(z–zo)=0.
Подставим данные: А(1; -2; 5), n = (2; -16; -13).
2·(x – 1) + (-16)· (y + 2) + (-13)·(z - 5) = 0.
2x - 2 - 16y - 32 - 13z + 65 = 0.
2х - 16y - 13z + 31=0.
О т в е т. 2х - 16y - 13z + 31 = 0.
1. Раскроем скобки в левой части выражения (правую часть оставляем без изменений):
х²+12х-12х-144 = 2(х-6)²-х²
2. Посмотрим внимательнее на правую часть. В правой части стоит квадрат разности, а это формулы сокращённого умножения. Привожу формулу квадрата разности:
(a-b)² = a²-2ab+b²
3. Теперь раскроем скобки в правой части выражения, применив данную формулу (левую часть оставим без изменений):
х²+12х-12х-144 = 2(х²-2·х·6+6²)-х²
4. Для удобства мы раскрыли скобки не до конца. Раскроем их окончательно (левую часть оставим без изменений):
х²+12х-12х-144 = 2х²-2·2·х·6+2·6²-х²
5. Преобразуем обе части получившегося выражения (приведём подобные слагаемые и т.д.):
х²-144 = 2х²-24х+72-х²
х²-144 = х²-24х+72
6. Обе части уравнения максимально упрощены. Решим его:
х²-х²+24х = 72+144
24х = 216
х = 216/24
х = 9
1) х1+х2=25
х1*х2=150
х1=10
х2=15
2) х1+х2=7
Х1*х2=-44
Х1=-4
Х2=11
3) (х+13)(х+7)
4) х1=-3, х2=-15
Объяснение:
1) х²-25х+150=0
D=625-600=25=5²
х1=(25-5)/2=10
х2=(25+5)/2=15
2) х²-7х-44=0
D=49+176=225=15²
Х1=-4
Х2=11
3) х²+20х+91=х²+13х+7х+91=х(х+13)+7(х+13)=(х+13)(х+7)
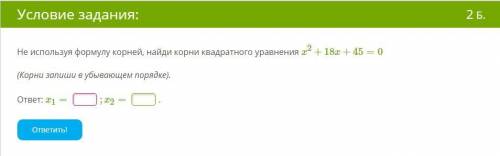
4)х²+18х+45=0
Х²+15х+3х+45=0
Х(х+15)+3(х+15)=0
(х+15)(х+3)=0
Х1=-3 или х2=-15