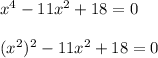
Выполним замену: 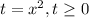
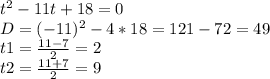
Выполним обратную замену:
t1:
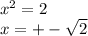
t2:
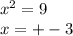
ответ: 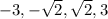 .
.
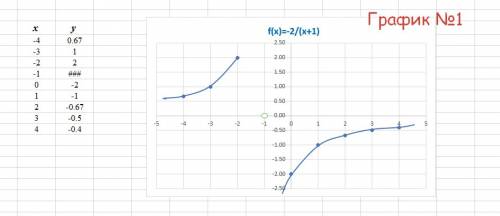
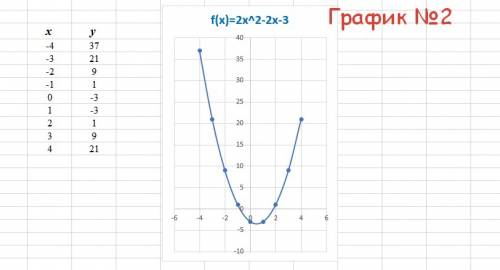
Задача имеет 2 решения
A(5;5) C(-5;-5) или A(-5;-5) C(5;5)
Объяснение:
Введу обозначение-(MN) это вектор MN
Точки B(−5; 5) и D(5; −5) центрально симметричны относительно начала координат О(0; 0), что совпадёт с центром симметрии квадрата. Значит и точки А и С симметричны относительно относительно точки О.
Пусть координаты точки А(x; y), тогда координаты точки С(-x; -y)
AC²=(-x-x)²+(-y-y)²==4x²+4y²
BD²=(-5-5)²+(-5-5)²=200
AC²=BD²
4x²+4y²=200
x²+y²=50
(CA)⊥(BD)⇒(AC)·(BD)=0
(CA)={2x;2y}; (BD)={10;-10}
0=(AC)·(BD)=10·2x+(-10)·2y=20x-20y⇒x-y=0⇒y=x
x²+x²=50
2x²=50
x²=25
x=±5⇒y=x=±5
A(5;5) C(-5;-5) или A(-5;-5) C(5;5)
x1 = ±3
x2 = ±√2
Объяснение:
x⁴ - 11x² + 18 = 0
Заменяем x² = y
y² - 11y + 18 = 0
D = (-11)² - 4 * 1 * 18 = 121 - 72 = 49 (7²)
y1 = (11 + 7)/2 = 18/2 = 9
y2 = (11 - 7)/2 = 4/2 = 2
Теперь подставляем обратно
x² = 9
x1 = ±3
x² = 2
x2 = ±√2