Деление многочленов в столбик
Старший одночлен делимого 2x⁴ делится на старший одночлен делителя x³
2x⁴ : x³ = 2x - это первое слагаемое частного.
Далее делитель (x³ + x - 2) почленно умножается на 2x и вычитается из делимого.
Старший оставшийся одночлен делимого 2x³ делится на старший одночлен делителя x³
2x³ : x³ = 2 - это второе слагаемое частного.
Далее делитель (x³ + x - 2) почленно умножается на 2 и вычитается из полученного многочлена.
Вторая степень многочлена остатка (-7x²+2x+2) меньше третьей степени делителя (x³ + x - 2) , поэтому деление окончено.
Частное (2x + 2), остаток (-7x²+2x+2)
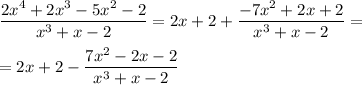
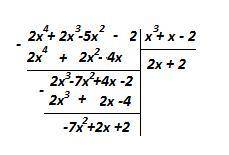
График на фотографии.
А) Найдем наибольшее и наименьшее значение функции на отрезке [-4;6]. Так как графиком функции является прямая, которая убывает на R, то для нахождения наибольшего и наименьшего значений достаточно подставить в функцию крайние точки промежутка.
у(-4) = (-1/2)*(-4) + 1 = 3
у(6) = (-1/2)*6 + 1 = -2
Значит, у наиб = 3, у наим = -2.
Б) -1/2x + 1 > 0
-1/2x > -1
х < 2.
у > 0 на промежутке (- бексконечность; 2)
ИЛИ
по графику видно, что у > 0 на промежутке (- бексконечность; 2)