(3,27)
Объяснение:
Переводим условие в алгебраическую форму
s - возраст сына, b - возраст батька
s + 24 = b
4(s +5) = b + 5
упростим второе уравнение
4s +20 - 5 = b
4s + 15 = b
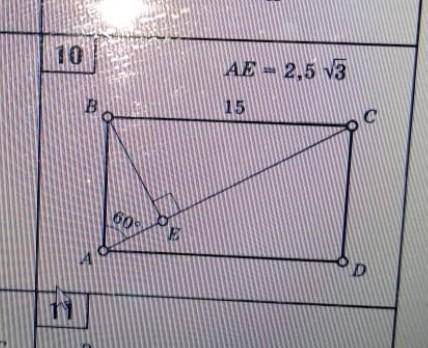
Осталось решить систему графическим образом. Лучше бы на миллиметровке, но если ее нет, то можно взять клетки в масштабе 1 - это полклетки.
График первого уравнения (прямую) построим по точкам:
s = 0 ; b =24
s = -24 ; b = 0
График второго уравнения (прямую) построим по точкам:
s = -4; b = 1
s = 0 ; b = 15
Прямые пересеклись в точке (3;27), то есть s = 3 это возраст сына, а b = 27 - возраст батька.
Объяснение:
1) a5 = a1 + 4d; a9 = a1 + 8d; a7 = a1 + 6d
{ a1 + a1 + 4d = 14
{ a1 + 8d - (a1 + 6d) = 4
Упрощаем
{ 2a1 + 4d = 14
{ 2d = 4
Получаем
{ d = 2
{ a1 + 2d = 7;
a1 = 7 - 2*2 = 3
2) b1 = 2; b4 = b1*q^3 = - 16
Отсюда
q^3 = - 16/b1 = - 16/2 = - 8
q = - 2
S(6) = b1*(q^6 - 1) / (q - 1) = 2*((-2)^6 - 1) / (-2 - 1) = 2*(64-1)/(-3) = - 2*63/3 = - 42
S(6) = - 42
3) Условие недописано, решить не могу.
4) b2 = b1*q = 4; b5 = b1*q^4 = - 32
Найти S(4).
{ b1*q = 4
{ b1*q^4 = - 32
Делим второе уравнение на первое уравнение
(b1*q^4) : (b1*q) = - 32 : 4
q^3 = - 8
q = - 2
Подставляем в первое уравнение
b1*(-2) = 4
b1 = 4/(-2) = - 2
S(4) = b1*(q^4 - 1)/(q - 1) = - 2*((-2)^4 - 1) / (-2 - 1) = - 2*(16-1)/(-3) = - 2*(-5) = 10
S(4) = 10