Объяснение:
Как я понял, задача состоит в нахождении наибольшего значения функции. Для это необходимо найти производную этой функции и приравнять ее к 0 .
Правила взятия производной, необходимые для решения этого примера:
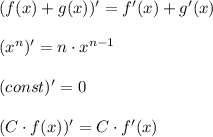
Эти правила можно описать следующим образом :
· Производная от суммы функций равна сумме их производных.
· Производная степенной функции равна произведению показателя степени на функцию, с показателем степени на 1 меньше исходного.
· Производная от постоянной величины равна 0.
· Постоянный множитель можно вынести за знак производной.
Тогда производная заданной функции равна :
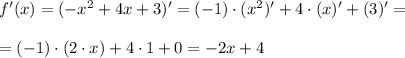
Приравняем производную к 0 и найдем корень уравнения:
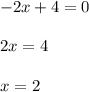
Подставим найденное значение в исходную функцию:
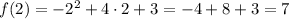
Получили, что наибольшее значение функции равно 7 в точке x=2
Из второго ур-ия выразить х (или у, без разницы) - и полученное выражение подставить в первое уравнение:
х=(15-3у)/4
(15-3у)^2/16 + y^2 = (15-3y-4)^2/16 +(y+3)^2 - домножим обе части ур-ия на 16 (чтобы избавиться от знаменателей)
(15-3y)^2 + 16y^2 = (11-3y)^2 + 16*(y+3)^2
225 - 90y +9y^2 + 16y^2 = 121-66y+9y^2 + 16y^2 + 96y + 144 - приводим подобные, перенеся все влево, справа будет 0.
225 - 90y +9y^2 + 16y^2 -121+66y-9y^2-16y^2-96y-144 =0
-40 -120у=0, 120у=-40,
у=-1/3, х=(15+1)/4=16/4=4
ответ: (4; 1/3)