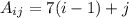(при движении в строке (меняя номер столбца) увеличиваем значение на 1, и изначально значение должно быть равно 1; при движении в столбце (изменяя номер строки) увеличиваем на 7, при этом изначально эта часть должна равняться 0)![S = [7(i_{1}-1)+j_{1}] + [7(i_{2}-1)+j_{2}] + [7(i_{3}-1)+j_{3}] + [7(i_{4}-1)+j_{4}] + [7(i_{5}-1)+j_{5}] + [7(i_{6}-1)+j_{6}] + [7(i_{7}-1)+j_{7}] = 7(i_{1}+i_{2}+i_{3}+i_{4}+i_{5}+i_{6}+i_{7}-7) + j_{1}+j_{2}+j_{3}+j_{4}+j_{5}+j_{6}+j_{7}](/tpl/images/0813/6728/e7629.png)
95 (руб.) стоит детский билет;
245 (руб.) стоит взрослый билет.
Объяснение:
Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 435 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 775 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?
х - детский билет
у - взрослый билет
По условию задачи составляем систему уравнений:
2х+у=435
3х+2у=775
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
у=435-2х
3х+2(435-2х)=775
3х+870-4х=775
-х=775-870
-х= -95
х=95 (руб.) стоит детский билет
у=435-2х
у=435-2*95
у=435-190
у=245 (руб.) стоит взрослый билет.
Проверка:
2*95+245=435
3*95+2*245=775, верно.
Даны точки А (3;-2;1), В(-2;1;3), C(1;3;-2).
Векторы: АВ = (-5 3; 2), модуль √(25 + 9 + 4) =√38.
АС = (-2; 5; -3), модуль √(4 + 25 + 9) =√38.
Их скалярное произведение равно -5*-2 + 3*5 + 2*-3 = 10 + 15 - 6 = 19.
cos(AB_AC) = 19/(√38*√38) = 19/38 = 1/2.
∠A = arc cos(1/2) = π/3.