Если z = 2, то либо x = 1, либо y = 0. Оба из этих чисел не являются простыми. Значит, z ≠ 2.
Если z — число нечётное, то — чётное. Учитывая, что x и y — простые числа, x может быть равен только 2, иначе это будет нечётным числом.
Попробуем поперебирать значения y:
2² + 1 = 5 — подходит,
2³ + 1 = 9 — не подходит,
2⁵ + 1 = 33 — не подходит,
2⁷ + 1 = 129 — не подходит...
Можно заметить, что при нечётных y z делится на 3. Всегда ли выполняется это условие?
Множество нечётных чисел включает в себя множество простых чисел (за исключением 2). Если , то и для простых чисел, кроме 2, это тоже справедливо.
Докажем это методом математической индукции:
1. При k = 1 утверждение верно (см. перебор, второе равенство).
2. Пусть — верно.
3.
Значит, 2 в любой нечётной степени (даже 2¹, которое мы упустили из доказательства) при делении на 3 даёт остаток 2. Отсюда справедливо выражение . Значит, z при всех простых y, отличных от 2, делится на 3, то есть не является простым числом. Отсюда получаем единственное найденное решение: x = 2, y = 2, z = 5.
Решение первое задание n^3+3n^2+5n+3 = (n^3+5n)+ (3n^2+3) =(n^3+5n)+ 3(n^2+1) второе слагаемое делится на 3 при любых n, осталось доказать, что первое слагаемое кратно 3 при любых n Разобьём все числа на три класса 1) 3к 2) 3к+1 3) 3к+2 Каждое натуральное число принадлежит какому-то одному классу 1) n^3+5n=(3к) ^3+5(3к) = 3 ( 9к^3)+5к) то есть числа этого класса являются делителями данного выражения 2) n^3+5n = (3к+1)^3+5(3к+1)= 27к^3+ 27к^2+9к+1+15к+5 = 27к^3+ 27к^2+24к+6 = 3( 9к^3+ 9к^2+8к+2) данное выражение делится на 3 и для чисел этого класса 3) n^3+5n = (3к+2)^3+5(3к+2)= = 27к^3+ 54к^2+36к+8+15к+10 = 27к^3+ 54к^2+51к+18 =3( 9к^3+ 18к^2+17к+6) данное выражение делится на 3 и для чисел вида (3к+2 ) вывод число (n^3+3n^2+5n+3) делится на 3 при любом n принадлещажее к N Второе задание 2n^3-3n^2+n = n( 2n^2-3n+1) = n(n-1)(2n-1) n(n-1)-это произведение двух последовательных натуральных чисел и одно из них делится на 2, значит выражение 2n^3-3n^2+n делится на 2 при любом n принадлещажее к N ( n>1) Самостоятельно докажи, как в первом примере, что данное выражение делится на 3 для этого нужно доказать делимость на 3 выражения 2n^3+n
Любое простое число, кроме 2, является нечётным.
Если z = 2, то либо x = 1, либо y = 0. Оба из этих чисел не являются простыми. Значит, z ≠ 2.
Если z — число нечётное, то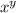
— чётное. Учитывая, что x и y — простые числа, x может быть равен только 2, иначе это будет нечётным числом.
Попробуем поперебирать значения y:
2² + 1 = 5 — подходит,
2³ + 1 = 9 — не подходит,
2⁵ + 1 = 33 — не подходит,
2⁷ + 1 = 129 — не подходит...
Можно заметить, что при нечётных y z делится на 3. Всегда ли выполняется это условие?
Множество нечётных чисел включает в себя множество простых чисел (за исключением 2). Если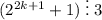
, то и для простых чисел, кроме 2, это тоже справедливо.
Докажем это методом математической индукции:
1. При k = 1 утверждение верно (см. перебор, второе равенство).
2. Пусть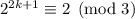
— верно.
3.
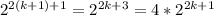
Значит, 2 в любой нечётной степени (даже 2¹, которое мы упустили из доказательства) при делении на 3 даёт остаток 2. Отсюда справедливо выражение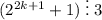
. Значит, z при всех простых y, отличных от 2, делится на 3, то есть не является простым числом. Отсюда получаем единственное найденное решение: x = 2, y = 2, z = 5.
ответ: (2; 2; 5)