1) Разность арифметической прогрессии: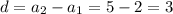 
. Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
2) Пятый член: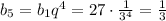 
Сумма четырех первых членов геометрической прогрессии:
3) Знаменатель прогрессии: 
Сумма бесконечно убывающей геометрической прогрессии:
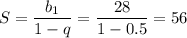
4) Здесь в условии опечатка, скорее всего d=-0.5, а если так как есть то задача решения не имеет.
ответ: 7
5) 
- геометрическая прогрессии
![b_4=b_1q^3~~\Leftrightarrow~~ q=\sqrt[3]{\dfrac{b_4}{b_1}}=\sqrt[3]{\dfrac{20}{2.5}}=2](/tpl/images/0269/0920/8578b.png)
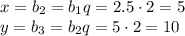
6) 6; 12; .... ; 96; 102; 108; .... ;198 - последовательность чисел, кратных 6.
Посчитаем сколько таких чисел:
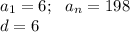
Сумма первых 33 членов а.п.: 
Нам нужно найти сумму всех натуральных чисел превышающих 100 и меньших 200 , которые кратны 6
, значит найдем сумму не превышающих 100 и отнимем от суммы не превышающих 200
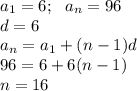
Искомая сумма: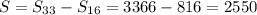 
1.
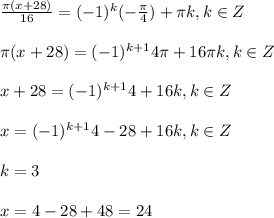
наименьший положительный х=24
2.
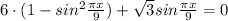
Квадратное уравнение относительно синуса
6t²-√3·t-6=0
D=3+144=147
√D=√(3·49)=7·√3
t₁=-√3/2; t₂=2√3/3 > 1
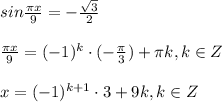
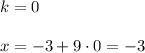
наибольший отрицательный
4.
Так как
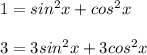
уравнение имеет вид:
2cos²x+6√3sinx·cosx+3sin²x+3cos²x=0
3sin²x+6√3sinx·cosx+5cos²x=0
Это однородное тригонометрическое уравнение.
Делим на cos²x≠0
3tg²x+6√3tgx+5=0
D=(6√3)²-4·3·5=108-60=48
√D=4√3
tgx=-5√3/3 или tgx=-√3/3
x=arctg(-5√3/3) +πk, k∈Z или x=arctg(-√3/3)+πn, n∈Z
Функция y=arctgx - монотонно возрастающая на (-∞;+∞)
-(5√3/3) < (-√3/3)⇒arctg(-5√3/3) < arctg(-√3/3)
Наибольший отрицательный
n=0
x=atctg(-√3/3)=-30°
1) Доманжаем на x обе части уровнения.
2)Возводим обе части в кавдрат
3)Переносим все влево, чтоб справа был 0
4)Решаем квадратное уровнение 576x^2+25x-125=0