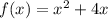
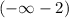
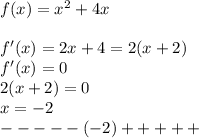
Производная отрицательна при х∈(-∞;-2)⇒функция убывает
Объяснение:
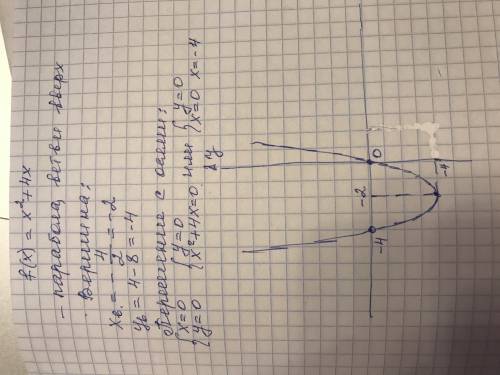
Объяснение:
1) х1 = -4, х2 = -3
х1 + х2 = -4 + (-3) = -4 - 3 = -7 = -b
х1*х2 = (-4)*(-3) = 4*3 = 12 = с
2) х1 = -1, х2 = 3
х1 + х2 = -1 + 3 = 2 = -b
х1*х2 = (-1)*3 = -1*3 = -3 = с
3) х1 = -4, х2 = -1
х1 + х2 = -4 + (-1) = -4 - 1 = -5 = -b
х1*х2 = (-4)*(-1) = 4*1 = 4 = с
4) х1 = -2, х2 = 4
х1 + х2 = -2 + 4 = 2 = -b
х1*х2 = (-2)*4 = -2*4 = -8 = с
5) х1 = 3, х2 = 5
х1 + х2 = 3 + 5 = 8 = -b
х1*х2 = 3*5 = 15 = с
6) х1 = -1, х2 = 4
х1 + х2 = -1 + 4 = 3 = -b
х1*х2 = (-1)*4 = -1*4 = -4 = с
7) х1 = -8, х2 = -2
х1 + х2 = -8 + (-2) = -8 - 2 = -10 = -b
х1*х2 = (-8)*(-2) = 8*2 = 16 = с
8) х1 = 2, х2 = 4
х1 + х2 = 2 + 4 = 6 = -b
х1*х2 = 2*4 = 8 = с
Объяснение:
Находим производную ф-ции: 2x+4
Находим критические точки, приравняв к нулю: 2x+4=0
x=-2;
Делаем небольшой рисунок и определяем знаки. Подставляем -3 вместо x и получаем -2, значит (-∞;-2) минус, ф-ция убывает. Подставляем 1, получаем 6, значит справа плюс. Если точка переходит с - на +, это точка минимума.