Объяснение:
x²+y²≤9
x²+y²≤3²
это часть плоскости внутри окружности с радиусом R=3 и центром в начале координат и сама окружность
2х-у≥1
2х-1≥у
у≤2х-1 это часть плоскости ниже прямой у=2х-1
x²+y²≤9
x²+y²≤3² это часть плоскости внутри и на границе окружности и ниже прямой
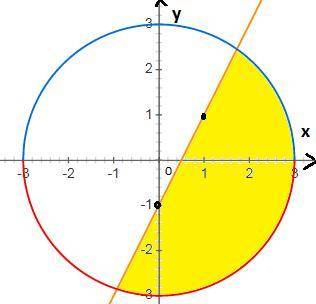
Построим окружность с центром в начале координат и радиусом R=3
Построим прямую у=2х-1 по двум точкам
х=0 у=2х-1=2*0-1=-1 (0;-1)
х=1 у=2х-1=2*1-1=2-1=1 (1;1)
выделим цветом часть плоскости внутри и на границе окружности и ниже прямой
Разложение многочлена на множители группировкиЕсли члены многочлена не имеют общего множителя, отличного от 1, то можно попытаться разложить такой многочлен группировки.Для этого надо объединить в группы те члены, которые имеют общие множители, и вынести за скобки общий член каждой группы. Если после таких преобразований окажется общий множитель у всех получившихся групп, то его вынести за скобки.
Разложить многочлен на множители: 10ay – 5cy +2ax-cx.1) Объединим в первую группу 10ay и 2ax, а во вторую группу -5cy и -cx: (10ay и 2ax) + (-5cy и -cx) .2) В первой группе вынесем за скобки общий множитель 2а, во второй группе вынесем за скобки общий множитель -с: 2а(5у+х)-с(5у+х).3) Как видим, оба члена многочлена имеют общий множитель (5y+х), вынесем его за скобки: (5y+х)(2а-с).Получим: 10ay – 5cy +2ax-cx= (5y+х)(2а-с).ответ а)м^2-2м+1-н^2-5н+25 б)(3+с)^2