Подставим значение переменной x, данное по условию, в уравнение и найдем значение c, решив полученное линейное уравнение с одной переменной:
2 * (-3)^2 + 7 * (-3) + c = 0;
2 * 9 – 21 + c = 0;
18 – 21 + c = 0;
c – 3 = 0;
c = 3.
Чтобы найти второй корень уравнения, данного по условию, подставим в него найденное значение c и решим полученное уравнение с одной переменной второй степени:
2 * x^2 + 7 * x + 3 = 0.
Найдем дискриминант:
D = 7^2 – 4 * 2 * 3 = 49 – 24 = 25.
x1 = (- 7 + 5)/(2 * 2) = - 2/4 = - 1/2;
x2 = (- 7 – 5)/(2 * 2) = - 12/4 = - 3.
ответ: c = 3; x = - 1/2.
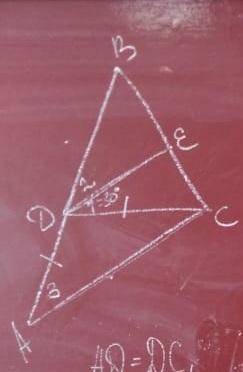
L3=30°
L2=30°
Объяснение:
DE||AC следует L1 = LECA ( накрест лежащие при параллельных прямых de ac и секущей cd.)
LECA=30°
Треугольник adc - равнобедренныц, т.к 2 стороны равны, следует LECA=L3
L3=30°
Т.К нам известны 2 угла, можем найти 3. Ladc=180°-30°-30°=120°
L2=180°-30°-120°=30°