Представте в виде квадрата двучлена : а) х2-12Х+36 Б)16а2+8аб+б2
в)0,81p2+0.72pg+0.16g2
г)1\25m2-4mn+100n2

👇

Увидеть ответ

Ответ:

justsgamer2000Kerzch

22.12.2021

а) х2-12Х+36 = (x - 6)^2

Б)16а2+8аб+б2 = (4a + b)^2

в)0,81p2+0.72pg+0.16g2 = (0,9p + 0,4g)^2

г)1\25m2-4mn+100n2 = (0,2m - 10n)^2

Объяснение:

^2 - это квадрат, если что

4,7(90 оценок)

Открыть все ответы

Ответ:

madinaseidahmet

22.12.2021

Пусть первый катет равен

см, тогда второй катет -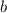

см. Площадь прямоугольного треугольника равна 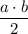$\dfrac{a\cdot b}{2}$ , что составляет 210 см² или перепишем сразу $a\cdot b=420$

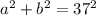
По теореме Пифагора: a^2+b^2=37^2

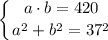
Составим и решим систему уравнений $\displaystyle \left \{ {{a\cdot b=420} \atop {a^2+b^2=37^2}} \right.$

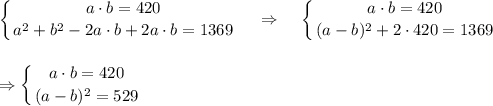
$\displaystyle \left \{ {{a\cdot b=420} \atop {a^2+b^2-2a\cdot b+2a\cdot b=1369}} \right. ~~~\Rightarrow~~~ \left \{ {{a\cdot b=420} \atop {(a-b)^2+2\cdot420=1369}} \right. ~~\\ \\ \\ \Rightarrow \left \{ {{a\cdot b=420} \atop {(a-b)^2=529}} \right.$

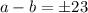Из второго уравнения имеем, что $\displaystyle a-b=\pm23$ . Тогда имеем несколько случаев.

Случай 1. Если a-b=23

, то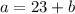

и подставим в первое уравнение.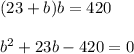
$(23+b)b=420\\ \\ b^2+23b-420=0$

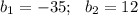Согласно теореме виета b_1=-35;~~ b_2=12

см и корень b_1

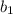не удовлетворяет заданному условию
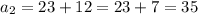a_2=23+12=23+7=35

см

Случай 2. Если a=b-23

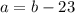,то подставив в первое уравнение, получим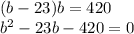

$(b-23)b=420\\ b^2-23b-420=0$
Согласно теореме Виета b_3=-12

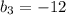
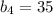см и корень b_3

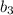не удовлетворяет условию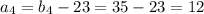
a_4=b_4-23=35-23=12

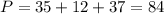Катеты прямоугольного треугольника равны 35 см и 12 см или 12 см и 35 см.

Периметр прямоугольного треугольника: P=35+12+37=84

см

ответ: 84 см.

4,4(96 оценок)

Ответ:

silvia16

22.12.2021

75°

Объяснение:

По условию считаем, что каждый друзей видит свой участок стены и друзья вместе контролируют только четвертую часть стены комнаты, что означает 90° (рисунок приложен). По обозначению эта стена дуга BE= дуга EC + дуга СВ = 90°.

Угол обзора одного из друзей ∠CDE=10°, а у другого ∠ВАС=20°, а их сумма ∠ВАС+∠CDE=10°+20°=30°.

Нужно определить градусную меру щели КМ, т.е. дуги КМ.

Применим следующую теорему о секущих:

Угол между двумя секущими, проведенными из одной точки, равен полу разности большей и меньшей высекаемых ими дуг.

Тогда ∠ВАС=(дуга СВ - дуга КМ)/2 и ∠CDE=(дуга EC - дуга КМ)/2.

Поэтому

∠ВАС+∠CDE=(дуга СВ - дуга КМ)/2+(дуга EC - дуга КМ)/2=

=(дуга EC + дуга СВ - 2•дуга КМ)/2=(90°-2•дуга КМ)/2

или же

(90°-2•дуга КМ)/2=30°

90°-2•дуга КМ = 60°

2•дуга КМ = 150°