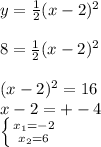
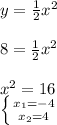
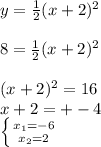
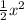 - расположен симметрично оси Y
- расположен симметрично оси Y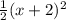 - график сдвинут по оси Х на 2 влево
- график сдвинут по оси Х на 2 влево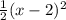 - график сдвинут по оси Х на 2 вправо
- график сдвинут по оси Х на 2 вправо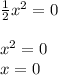
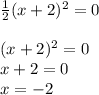
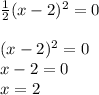
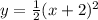 x∈
x∈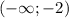
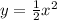 x∈
x∈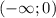
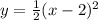 x∈
x∈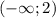
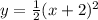 x∈
x∈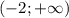
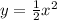 x∈
x∈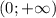
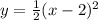 x∈
x∈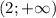
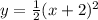 x=-2
x=-2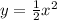 x=0
x=0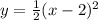 x=2
x=2

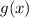 ;
; ;
; и будет искомой фигурой.
и будет искомой фигурой.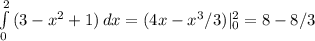
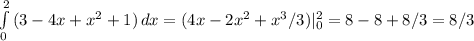
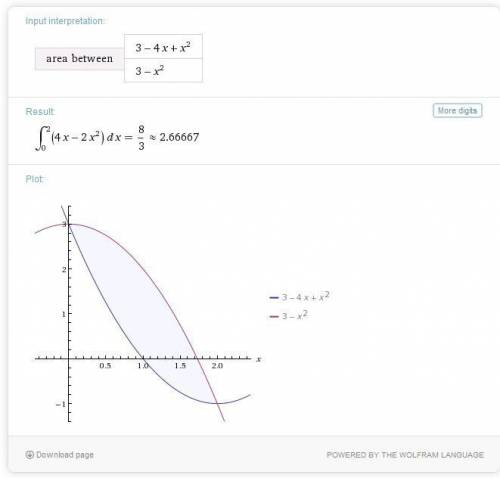
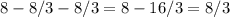 (кв. ед.)
(кв. ед.)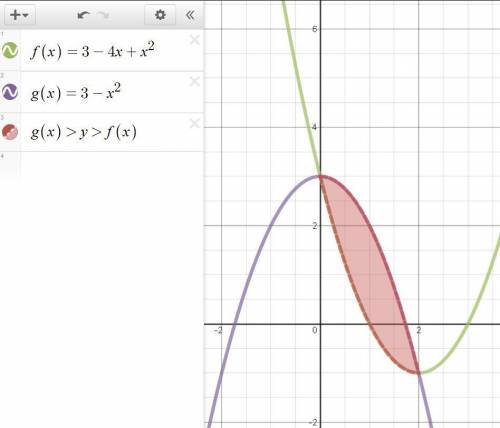
|х - 2| < 5
откуда -3<x<7 Протяженность интервала=10
х2 - 16 > 0
Откуда х<-4 и х>4
х<-4 не подходит к 1 неравенству.
Протяженность интервала, удовлетворяющая первому неравенству, равна 3 (от 4 до 7).
Тогда вероятность равна 3/10 (протяженность интервала рашения совместно 1 ого и 2ого неравенства, деленная на протяженность интервала 1 неравенства)