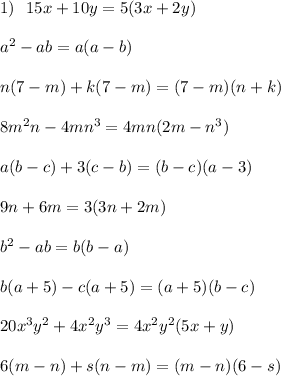
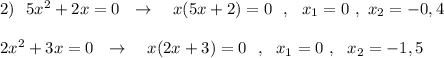
Пусть х км/ч - собственная скорость лодки, тогда (х + 1) км/ч - скорость лодки по течению реки, (х - 2) км/ч - скорость лодки против течения реки. Уравнение:
24/(х+1) + 12/(х-1) = 5
24 · (х - 1) + 12 · (х + 1) = 5 · (х + 1) · (х - 1)
24х - 24 + 12х + 12 = 5 · (х² - 1²)
36х - 12 = 5х² - 5
5х² - 5 + 12 - 36х = 0
5х² - 36х + 7 = 0
D = b² - 4ac = (-36)² - 4 · 5 · 7 = 1296 - 140 = 1156
√D = √1156 = 34
х₁ = (36-34)/(2·5) = 2/10 = 0,2 - не подходит по условию задачи
х₂ = (36+34)/(2·5) = 70/10 = 7 км/ч - скорость лодки
Вiдповiдь: 7 км/год - власна швидкiсть човна.
18 (км/час) - скорость первого велосипедиста
24 (км/час) - скорость второго велосипедиста
Объяснение:
х - скорость первого велосипедиста
х+6 - скорость второго велосипедиста
24/х - время первого велосипедиста
24/(х+6) - время второго велосипедиста
По условию задачи разница во времени велосипедистов 20 минут, это 20/60=1/3 (часа), уравнение:
24/х - 24/(х+6) =1/3
Избавляемся от дробного выражения, общий знаменатель 3х(х+6), надписываем над числителями дополнительные множители:
24*3(х+6)-24*3х=1*х(х+6)
72х+432-72х=х²+6х
432=х²+6х
-х²-6х+432=0
х²+6х-432=0
х₁,₂=(-6±√36+1728)/2
х₁,₂=(-6±√1764)/2
х₁,₂=(-6±42)/2
х₁= -48/2= -24 отбрасываем, как отрицательный
х₂=36/2=18 (км/час) - скорость первого велосипедиста
18+6=24 (км/час) - скорость второго велосипедиста
Проверка:
24 : 18 = 1 и 1/3 (часа)= 1 час 20 минут, время первого велосипедиста
24 : 24 = 1 (час) - время второго велосипедиста
1 час 20 минут -1 час =20 минут разница, всё верно.