Всего на хоккей ходят 17 человек, из них 6 так же ходят на лыжи, 2 на коньки и 1 ходит и на коньки и на лыжи, а чисто хоккеистов 8.
Из всех лыжников 6 занимаются хоккеем
3-коньки
1 и лыжи и коньки
Т.е. 4 лыжников также занимаются коньками
Из коньков 5 занимаются двумя секциями: и из них уже известно, что 3 - лыжами, значит еще 2 - хоккеем
Т.о. из 13 коньков: 3 лыжников, 2 хоккеистов, 1 лыже-хоккеист и 7 чисто коньков
Значит всего тех, кто ходит на коньки, но при этом не ходит на лыжи 7+2=9 человек
В двух секциях будет 21+9=30 человек, значит чисто хоккеистов будет 38-30=8 человек
Прибавим к этим 8, еще 6-из лыжников, 2 коньков и 1 лыже-конька и получим 8+6+2+1=17
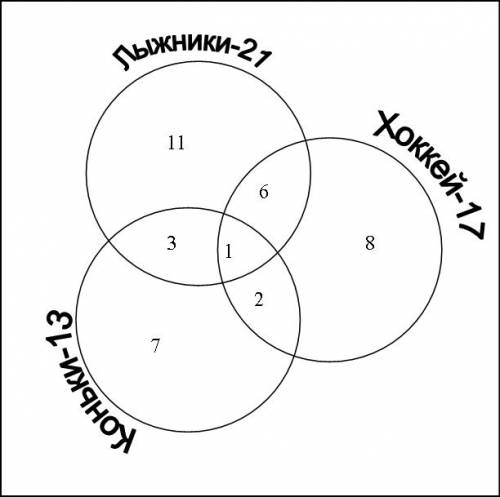
См. рисунок
б) в точках пересечения с осью абсцисс, ордината равна 0, т.е. нужно решить уравнение
3х^2+6x-9=0
x^2+2x-3=0
По теореме Виета:
x1+x2=-2
x1*x2=-3
Следовательно, х1=-3, х2=1 - это и есть искомые координаты точек пересечения параболы с осью абсцисс.
в) Так как коэффициент при x^2 равен 3, что больше 0, значит ветви параболы направлены вверх. Следовательно, наименьшее значение функция достигает в точке, которая является вершиной параболы. Найдем вершину:
х=-в/2а=-6/2*3=-1.
Значит функция достигает своего минимума в точке х=-1 и равна:
у(-1)=3-6-9=-12.
г) Строится парабола по трем точкам, которые мы нашли выше: вершина (-1;-12) и точки пересечения с осью Ох (-3;0) и (1;0)
Объяснение:
(х-4)^2-2х(х-2) = х^2-16-2х^2+4= -х^2-12
Умногим получившиеся выражение на -1. Получим х^2+12