Объяснение:
Проверим случай p=5, уйдет квадратичная часть, но линейная останется, значит неравенство не будет выполняться для всех x.
При p не равном 5 график левой части неравенства представляет собой параболу, для того, чтобы неравенство было верно для любого x вся парабола должна лежать ниже оси абсцисс, т. е. ветви вниз(p-5<0) и D(дискриминант)<0.
D1=(2p-4)^2-4(p-5)(-p-3)=8p^2-24p-44<0
2p^2-6p-11<0
D2=36+88=124
p1=(3-sqrt(31))/2
p2=(3+sqrt(31))/2
D1<0 при
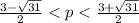
Эти значения p меньше пяти(т.е. ветви направлены вниз). Заносим их в ответ.
Будет сыграно С (2,18)*2=18*17/2*2=306 матчей.
В одном из предыдущих ответов не учтено, что в каждом матче участвуют ДВЕ команды, поэтому, если бы проводилось по одному матчу, то матчей было бы 18*17/2=153=(С (2,18), а поскольку они проводят по 2 матча - то в два раза больше. Элементарная задача на комбинаторику. А те ответы, где написано полная чушь.
Примечание: С (2,18) - так обозначается в комбинаторике число комбинаций при выборе двух элементов из 18 возможных. Оно равно 18!/(2!*(18-2)!)=18!/(2!*16!)=18*17/(2*1)=18*17/2=153
Объяснение: