Объяснение:
(х-5)^2<корень7(х-5)
(х-5)^2-корень7(х-5)<0
(х-5)×(х-5-корень7) <0
{х-5<0
{х-5-корень7>0
{х-5>0
{х-5-корень7<0
{х<5
{х>5+корень7
{х>5
{х<5+корень7
Х нет обьдинения
Х€( 5; 5+ корень7)
ответ : х€( 5; 5+корень7)
х₁= -√6 (≈ -2,5)
х₂=√6 (≈2,5)
Объяснение:
Координаты вершины параболы (0; -3), значит, х₀= 0, отсюда b=0; у₀= -3, отсюда с= -3.
Уравнение параболы у=ах²+bх+с.
Подставляем в уравнение известные значения х и у (координаты точки D(6; 15) и вычисляем а. Уже известно, что b=0, а с= -3:
15=а*6²+0*6-3
15=36а-3
-36а= -3-15
-36а= -18
а= -18/-36
а=0,5
Уравнение принимает вид: у=0,5х²-3
Решаем квадратное уравнение, находим корни, которые являются точками пересечения параболой оси Ох:
0,5х²-3=0
0,5х²=3
х²=6
х₁,₂= ±√6
х₁= -√6 (≈ -2,5)
х₂=√6 (≈2,5)
x€(5;5+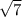
)
Объяснение:
(x-5)²<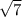
(x-5); переносим левую часть на правую с противоположным знаком
(x-5)²-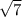
(x-5)<0; выносим за скобку х-5 и получим: (x-5)*((x-5)-
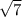)<0
(x-5)*(x-5-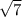
)<0; теперь методом интервала решаем неравенство и получим: 5<x<5+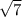
x€(5;5+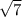
)