(здесь )Данное квадратное уравнение имеет 1 корень, если дискриминант D=0. Однако, если уравнение имеет 2 решения, причем разного знака, то нам подходит только одно положительное. Следовательно, в этом случае исходное уравнение будет иметь тоже 1 корень. Поэтому рассматриваем случай, когда
Тогда
Далее пусть меньший корень будет < 0, а больший >0.
Необходимо рассмотреть 3 случая:
1)
Тогда D>1, следовательно a<0. Получаем нет решений.
2)
Тогда всегда выполняется.
Тогда D>1, следовательно a<0.
3)
Таким образом и
б) неравенство будет иметь хотя бы один решение, если . Отсюда получаем a из
С Т О 1 3 9 2 7 8 4 1 7 6 9 5 8 3 4 9 7 3 - вот все возможные цифры, которые может принять число СТО.
ВОРОН + ___СТАЯ__ ЛЕТЕЛА
Смотрим на сумму. Буква В получается с переходом на десяток О+С=В >9. (получается из В сразу 2 буквы) Т.к. у нас сложение и не может быть более 9+8=17(9 и 9 не может быть, т.к. буквы разные), то к В мы прибавляем только 1. Чтобы перевалить за десяток при прибавлении 1 --- это может быть только 9. (9+1=10). Получаем: В=9 ЛЕ --- 10 Л=1 Е=0
Получаем вот такой вид 9ОРОН + ___СТАЯ__ 10Т 01А
Там, где подобраны числа СТО -- убираем 9 и 1. Остаются числа 278 и 834. (СТО) О+А - заканчивается на 1, это может быть =11 или 10+1, если Н+Я>10 Значит, Р+Т - заканчивается на 0, значит либо =9( и +1), либо =10. В любом случае, следующая сумма будет переходит десяток. (А О+С итак его переходят ---В.) О+С=Т>10 (и так же +1 от Р+Т)
Подбираем из оставшихся чисел С Т О 2 7 8 -- явно не подходит, т.к. 8+2=10.
С Т О 8 3 4 8+4=12 - последняя 2, теперь +1(от перехода на десяток предыдущей суммы Р+Т) 2+1=3 (единица уходит на В) Получаем: С=8 Т=3 О=4 В=9 Л=1 Е=0
9 4 Р 4 Н + ___ 8 3 А Я__ 10 3 0 1 А
4+А= либо 11, либо 10 (+1, если Н+Я >10) А=7 или 6 Р+3=9, т.к. добавляем +1,от перехода на десяток, поэтому у нас стоит 0. Р=9-3=6, значит А=7 Получаем 9 4 6 4 Н + ___ 8 3 7 Я__ 10 3 0 1 7
Т.к. 4+7=11, --последняя 1, то Н+Я<10 Подбираем оставшиеся числа 1=Л 2= 3=Т 4=О 5= 6=Р 7=А 8=С 9=В
5 +2=7 - верно. И нет никакой разницы, можно подставить и Н и Я. Пусть Н=5 Я=2. 9 4 6 4 5 + ___ 8 3 7 2__ 10 3 0 1 7 - --- ВЕРНО.
а) Рассмотрим уравнение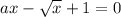
(a=0 подходит тогда х=1)сделаем замену переменных 
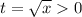. Получим уравнение
Далее пусть меньший корень будет < 0, а больший >0.
Необходимо рассмотреть 3 случая:
1)
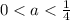
2)
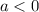
3)
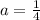
Таким образом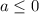
и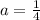 
б) неравенство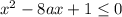
будет иметь хотя бы один решение, если 
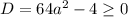. Отсюда получаем a из ![(-\infty ; -\frac{1}{4}]\cup{[\frac{1}{4};+\infty)}](/tpl/images/0040/0927/4f9da.png)