Нехай за 
год перший робітник виконає завдання, а за 
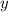год — другий. Тоді за одну годину перший робітник виконає 
усього завдання, а другий робітник — 
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто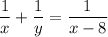 
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто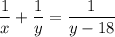 
Складаємо систему з двох рівнянь:
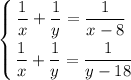
Тут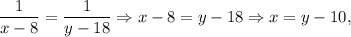 
оскільки ліві частини рівнянь рівні.
Підставимо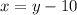 
в перше рівняння:
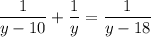
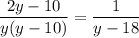
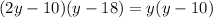
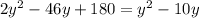
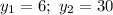
Якщ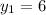о 
, то 
— не відповідає сенсу задачі.
Якщ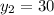о 
, то 
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.
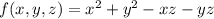
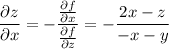
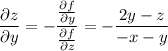
с координатами 
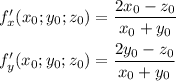
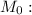
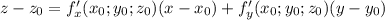- уравнение касательной в общем виде.
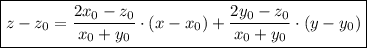- уравнение касательной плоскости к поверхности в точке с координатами 
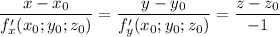
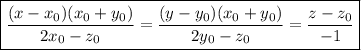- каноническое уравнение нормали к поверхности в точке с координатами
Только вариант Б)
В остальных то квадрат то дробь