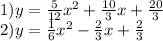
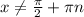
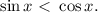
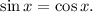Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от 
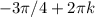до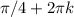 
.
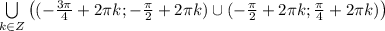
Вариант 3.
Объяснение:
Тождественное, т.е. тоже самое, схожее. Если убрать минус снизу у -5b-6y и поставить его перед числителем (см картинку мою), то получится -2x+a/6b+6y.
Знак "-" перед дробью можно внести либо в числитель, либо в знаменатель, но не туда и туда (иначе это будет уже 2 знака минус, т. е. в итоге - плюс) .
Мы вынесли минус в знаменателе и сделали его перед дробью, а потом внесли в числитель, в знаменателе естественно поменялись знаки, раз минус вынесли и в числители тоже, т.к. туда минус внесли.