x∈(0;1/5)∪(25;∞)
Объяснение:
ОДЗ: x>0
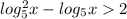- логарифмическое квадратное неравенство, замена переменной:
log₅x=t,
t²-t>2, t²-t-2>0 -метод интервалов:
1. t²-t-2=0, t₁= - 1, t₂= 2
2. + - +
-----------(- 1)-----------(2)---------------->t
3. t<-1, t>2
обратная замена:
1. t<-1, log₅x<-1, log₅x<log₅5⁻¹, log₅x<log₅(1/5)
основание логарифма а=5, 5>1, =. знак неравенства не меняем:
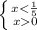
x∈(0; 1/5)
2. t>2, log₅x>2, log₅x.log₅5², log₅x>log₅25
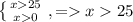
x∈(25;∞)
x∈(0;1/5)∪(25;∞)
1) Разность арифметической прогрессии: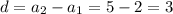 
. Тогда по формуле n-го члена арифметической прогрессии, найдем четырнадцатый член:
2) Пятый член: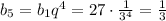 
Сумма четырех первых членов геометрической прогрессии:
3) Знаменатель прогрессии: 
Сумма бесконечно убывающей геометрической прогрессии:
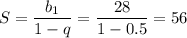
4) Здесь в условии опечатка, скорее всего d=-0.5, а если так как есть то задача решения не имеет.
ответ: 7
5) 
- геометрическая прогрессии
![b_4=b_1q^3~~\Leftrightarrow~~ q=\sqrt[3]{\dfrac{b_4}{b_1}}=\sqrt[3]{\dfrac{20}{2.5}}=2](/tpl/images/0269/0920/8578b.png)
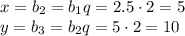
6) 6; 12; .... ; 96; 102; 108; .... ;198 - последовательность чисел, кратных 6.
Посчитаем сколько таких чисел:
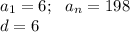
Сумма первых 33 членов а.п.: 
Нам нужно найти сумму всех натуральных чисел превышающих 100 и меньших 200 , которые кратны 6
, значит найдем сумму не превышающих 100 и отнимем от суммы не превышающих 200
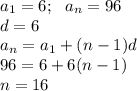
Искомая сумма: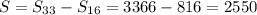 
определение модуля:
|х| = х, если х >= 0
|х| = -х, если х < 0
(модуль ---число положительное, а в самом х как бы содержится знак минус ---ведь х отрицательный...)
исходя из этого, важно определить корни подмодульного выражения ---значения х, обращающие модуль в 0
| x-2 |- |x+1 | +x-2
два корня: 2 и -1
значит, нужно рассматривать три интервала: (-беск.; -1) и [-1; 2) и [2; +беск)
---при переходе через корень подмодульное выражение поменяет знак... ---это ВАЖНО... при раскрытии модуля 1) (-беск.; -1)здесь (x-2) отрицательно, => |x-2| = -(x-2) = -х + 2
(x+1) ---тоже отриц. => |x+1| = -(х+1) = -х - 1
получим -х+2 - (-х-1) + х-2 = х + 1 для х из (-беск.; -1) 2) [-1; 2) здесь (x-2) отрицательно, => |x-2| = -х + 2
(x+1) --- положительно => |x-3| = х + 1
получим -х+2 - (х+1) + х-2 = -х - 1 для х из [-1; 2) 3) [2; +беск)
здесь (x-2) положительно, => |x-2| = x - 2
(x+1) ---тоже полож. => |x+1| = х + 1
получим х-2 - (х+1) + х-2 = х - 5 для х из [2; +беск)
получится ломаная линия... две прямые у = 0 и у = -3 будут иметь с нею ровно 2 общие точки т.е. m = 0 и m = -3