

 ∪
∪
 ∪
∪

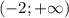
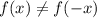
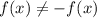

1.Задание
х² - 12х + 5 = 0
а) Если данное квадратное уравнение имеет два корня, то они имеют одинаковые знаки, так как по теореме Виета для них должно выполняться равенство x₁·x₂ = 5, которое возможно при либо положительных x₁ и x₂, либо при отрицательных х₁ и х₂.
б) По теореме Виета для х₁ и х₂ должно выполняться равенство
x₁+x₂ = 12, которое возможно при положительных x₁ и x₂.
ответ под цифрой 1) Оба положительные.
2.Задание.
х² + 3х -18 = 0
3·6=18;
а) x₁·x₂ = -18 => x₁ и x₂ имеют разные знаки:
-3·6= -18; или 3·(-6)= -18;
б) x₁+x₂=-3 => -3+6=3; или 3+(-6)=-3
ответ под цифрой 1) {-6; 3}.
3.Задание.
х² - 2х -24 = 0
4·6=24;
а) x₁·x₂ = -24 => x₁ и x₂ имеют разные знаки:
-4·6= -24; или 4·(-6)= -24;
б) x₁+x₂=2 => -4+6=2; или 4+(-6)=-2
ответ под цифрой 1) {-4; 6}.
4.Задание.
х² - 12х +20 = 0
2·10=20;
а) x₁·x₂ = 20 => x₁ и x₂ имеют одинаковые знаки:
2·10= 20; или -2·(-10)= 20;
б) x₁+x₂=12 => 2+10=20; или -2+(-10)=20
ответ под цифрой 1) {2; 10}.
5.Задание.
х² +ах - 12 = 0
х₁=2
а) x₁·x₂ = -12 => x₁ и x₂ имеют разные знаки:
2·(-6)= - 12; => х₂= -6
б) x₁+x₂=а => а=2+(-6)= -4
ответ под цифрой 4) х₂=-6; а= - 6.
6.Задание:
2х² + 10х + q =0
Делим обе части уравнения на 2 и получаем приведенное квадратное уравнение:
х² + 5х + q/2 =0 =>
х₁>x₂ на 3 => x₁ = x₂+3
а) По теореме Виета для х₁ и х₂ должно выполняться равенство:
x₁+x₂ = -5
Подставим x₁ = x₂+3 в это уравнение:
х₂+3 + х₂ = -5
2х₂= -5-3
2х₂= -8
х₂ = -8 : 2
х₂ = -4
б) x₁ = -4+3
x₁ = -1
в) По теореме Виета для х₁ и х₂ должно выполняться равенство:
x₁ · x₂ = q/2
q/2 = -1 · (-4)
q/2 = 4
q= 4·2
q=8
ответ под цифрой 1) q = 8 при х= -4 и х= -1.
у=х²-2х
х(верш)=-в/2а=2/2=1
у(верш)=у(1)=1-2=-1
Вершина: (1,-1)
Пересечение с ОХ: у=0 , х²-2х=0 , х(х-2)=0 . х=0 или х=2 ⇒ (0,0) или (2,0)
Пересечение с ОУ: х=0 , у=0-0=0 ⇒ (0,0)