Найдем, в каких пределах может изменяться сума цифр трехзначного числа:
- минимальная сумма цифр равна 1 (у числа 100)
- максимальная сумма цифр равна 27 (у числа 999)
Найдем наибольшую сумму цифр среди чисел от 1 до 27. Очевидно, что нужно по возможности максимально увеличить разряд единиц и разряд десятков. Таким образом, образуется два кандидата: числа 19 и 27.
- сумма цифр числа 19 равна 1+9=10
- сумма цифр числа 27 равна 2+7=9
Итак, наибольшая сумма цифр суммы цифр равна 10. Значит, искомая сумма цифр равна 19.
Трехзначные числа с суммой цифр 19 можно разделить на две группы: содержащие одинаковые цифры и не содержащие одинаковые цифры.
Рассмотрим случай, когда в записи числа используются одинаковые цифры:
9-9-1, 9-5-5, 8-8-3, 7-7-5, 7-6-6 - итого 5 случаев, для каждого из которых существует перестановок цифр указать место для уникальной цифры). Всего для этих вариантов имеем 5·3=15 чисел
Рассмотрим случай, когда в записи числа не используются одинаковые цифры:
9-8-2, 9-7-3, 9-6-4, 8-7-4, 8-6-5 - итого, 5 случаев, для каждого из которых существует перестановок цифр. Всего для этих вариантов имеем 5·6=30 чисел
Таким образом, всего есть 15+30=45 чисел, удовлетворяющих поставленному условию.
ответ: 45
Возьмем приближенно 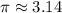
Рассмотрим число  . На числовой окружности этому числу соответствует та же точка, что и числу
. На числовой окружности этому числу соответствует та же точка, что и числу  :
:
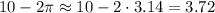
Зная, что 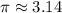 и
и 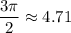 , получаем, что число
, получаем, что число 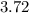 располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.
располагается в 3 четверти. Значит, можно сказать о знаках тригонометрических функций: косинус и синус - отрицательный, тангенс и котангенс - положительный. Остается сравнить между собой данные две пары.
Заметим, что число 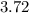 располагается ближе к числу
располагается ближе к числу 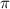 , так как
, так как 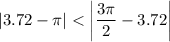 .
.
Зарисуем схематично число в 3 четверти, расположенное ближе к числу  . По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):
. По рисунку определим, что косинус такого числа (координата х) меньше синуса (координата y):
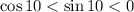
Рассмотрим тангенс. Так как тангенс положительный, то заменим отношение синуса к косинусу отношением их модулей:
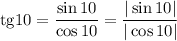
Зная, что 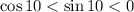 , получим, что
, получим, что 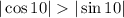 , соответственно дробь
, соответственно дробь 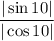 правильная, значит
правильная, значит 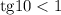 . Тогда, так как котангенс есть величина, обратная тангенсу, то
. Тогда, так как котангенс есть величина, обратная тангенсу, то 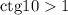 .
.
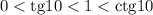
Итоговая цепочка: 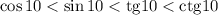
Воспользуемся формулами комбинаторики.
Во-первых, у нас имеется два места на латинские буквы, коих 26. Число вариантов считается как 26^2=676
Во-вторых, у нас имеется 4 места для цифр, коих 10. Итак: 10^4=10000
В итоге у нас 676*10000=6760000 вариантов.