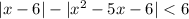
Преобразуем второй модуль и определим нули подмодульных выражений:
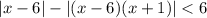
Нули подмодульных выражений: 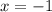 и
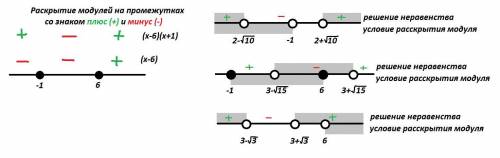
и  , поэтому раскрывать модуль будем на следующих промежутках:
, поэтому раскрывать модуль будем на следующих промежутках:
1) 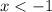
2) 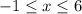
3) 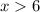
1) Раскрываем модуль на промежутке 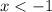 . Первый модуль раскрывается со сменой знака, второй - без смены знака:
. Первый модуль раскрывается со сменой знака, второй - без смены знака:
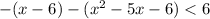
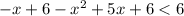
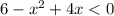
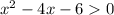
Найдем корни соответствующего уравнения:
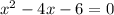
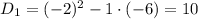
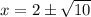
Методом интервалов найдем решение неравенства:
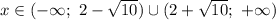
Учтем условие раскрытия модуля. Для этого сравним числа 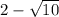 и
и 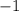 :
:
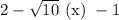
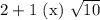
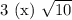
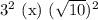
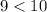
Значит, первое число меньше. Тогда, учитывая условие раскрытия модуля, получим:
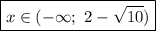
2) Раскрываем модуль на промежутке 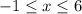 . Оба модуля раскрываются со сменой знака:
. Оба модуля раскрываются со сменой знака:
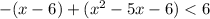
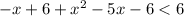
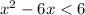
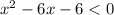
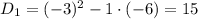
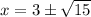
Методом интервалов найдем решение неравенства:
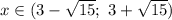
Учтем условие раскрытия модуля. Сравним числа 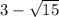 и
и 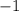 :
:
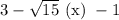
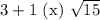
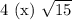
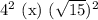
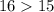
Первое число больше.
Сравним числа 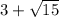 и
и 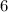 :
:
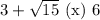
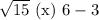
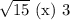
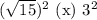
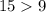
Первое число больше.
Теперь, учитывая условие раскрытия модуля, получим:
![\boxed{x\in(3-\sqrt{15} ;\ 6]}](/tpl/images/1359/2965/c2c24.png)
3) Раскрываем модуль на промежутке 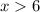 . Оба модуля раскрываются без смены знака:
. Оба модуля раскрываются без смены знака:


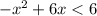
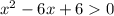
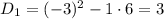
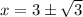
Используя метод интервалов, запишем решение неравенства:
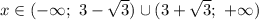
Число 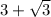 меньше числа
меньше числа 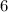 .
.
Запишем решение, учитывая условие раскрытия модуля:
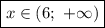
Итоговое решение неравенства представляет собой объединений трех промежутков:
![x\in(-\infty;\ 2-\sqrt{10} )\cup(3-\sqrt{15} ;\ 6]\cup(6;\ +\infty )](/tpl/images/1359/2965/d5f99.png)
Упростив запись, получим:
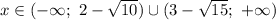
ответ: 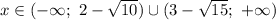
ответ: 2
Объяснение:
(1+ax)/(1-ax) *( (1-a^2*x^2)/(1+2ax+a^2*x^2) +√( (1-b*x)/(1+b*x) ) )
Упростим:
(1-a^2*x^2)/(1+2ax+a^2*x^2) = (1-a*x)*(1+a*x)/(1+ax)^2 = (1-ax)/(1+ax)
(1+ax)/(1-ax) *( (1-ax)/(1+ax) + √( (1-b*x)/(1+b*x) ) ) =
= 1+ ( (1+ax)/(1-ax) ) * ( √( (1-b*x)/(1+b*x) ) )
x = 1/a * √( (2a-b)/b ) = 1/a * √( 2a/b -1)
a*x = √( 2a/b -1)
b*x =b/a * √( 2a/b -1)
Для удобства обозначим : √( 2a/b -1) = t, тогда
2a/b = t^2 +1
b/2a = 1/(t^2+1)
b/a = 2/(t^2+1)
a*x = t
b*x = 2t/(t^2+1)
1+b*x = 1+2t/(t^2+1) = (t^2+2t+1)/(t^2+1) = (t+1)^2/(t^2+1)
1-b*x = 1- 2t/(t^2+1) = (t^2-2t+1)/(t^2+1) = (t-1)^2/(t^2+1)
√( (1-b*x)/(1+b*x) ) =√( (t-1)^2/(t+1)^2 ) = |(t-1)|/|(t+1)|
1+ ( (1+ax)/(1-ax) ) * ( √( (1-b*x)/(1+b*x) ) ) = 1 +( (1+t)/(1-t) ) * |(t-1)|/|(t+1)|
Из условия : 2a<=b<a<0 или 0<a<b<=2a следует, что
1<=2a/b <2a/a = 2
0<=2a/b -1<1
0<= t < 1
-1<=t-1<0 → |(t-1)| = 1-t
1<=t+1 <2 → |t+1| = 1+t
Таким образом :
1 +( (1+t)/(1-t) ) * |(t-1)|/|(t+1)| = 1 + 1 = 2