
Собственная скорость лодки 9 км/ч, скорость течения 1-ой реки 3 км/ч.
Даны три участка пути:
1-ая река,озеро,2-ая река.
Так как в озере нет течения, то лодка плывёт по нему с собственной скоростью, тогда
18:2=9 (км/ч)-собственная скорость лодки
Пусть х(км/ч) -скорость течения 2-ой реки, тогда скорость течения
1-ой реки х+2 (км/ч).
9-х (км/ч)-скорость движения лодки против течения по второй реке
9+х+2=11+х (км/ч)- скорость движения по течению по первой реке.
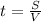 время движения
время движения
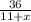 время движения по 1-ой реке
время движения по 1-ой реке
 время движения по 2-ой реке
время движения по 2-ой реке
2 ч -время движения по озеру
Так как общее время в пути 7 часов, то составим уравнение:
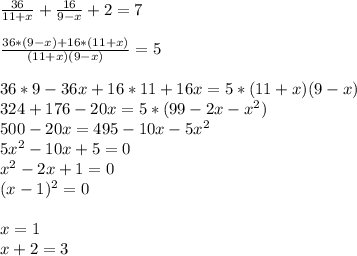
Скорость течения 1-ой реки равна 3 (км/ч).
ответ: 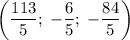
Объяснение:
Решить систему методом Крамера:
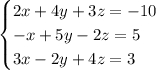
Найдем главный определитель системы:
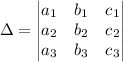
где a, b, c - числовые коэффициенты при x, y, z соответственно.
Найдем определитель разложением по первой строке:
Δ = a₁ · (b₂c₃ - b₃c₂) - b₁ · (a₂c₃ - a₃c₂) + c₁ · (a₂b₃ - a₃b₂)
Вычислим Δ:
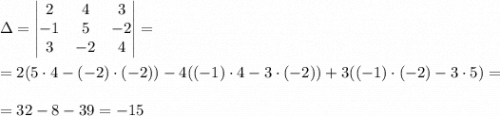
Δ ≠ 0 ⇒ система имеет единственное решение.
Для нахождения корней необходимо вычислить еще три определителя:
1. Δх.
Заменим в главном определителе первый столбец на столбец свободных членов (d):

Вычислим Δх:
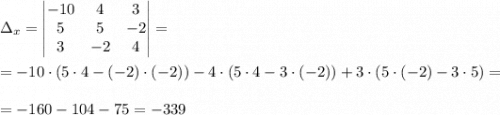
2. Δy.
Заменим в главном определителе второй столбец на столбец свободных членов (d):
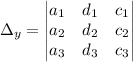
Вычислим Δy:
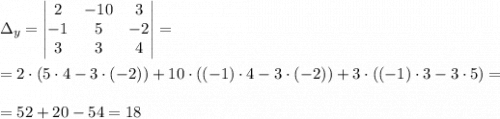
3. Δz.
Заменим в главном определителе третий столбец на столбец свободных членов (d):
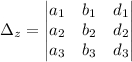
Вычислим Δz:
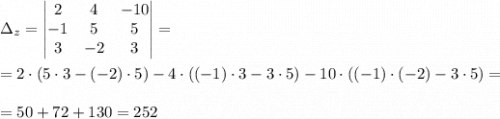
ответ рассчитывается по формулам:
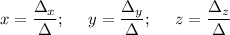
Найдем корни:
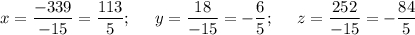
ответ: 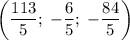
#SPJ1
решение смотри на фотографии
Объяснение: