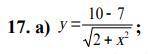
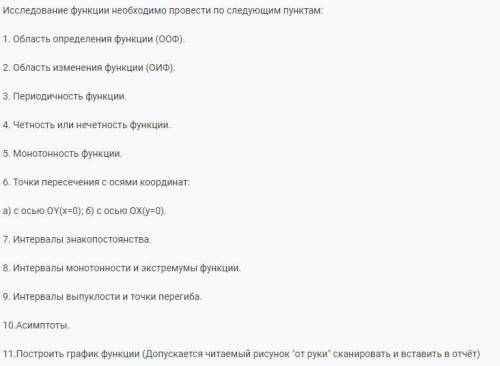
25 км/ч скорость лодки в неподвижной воде.
Объяснение:
Плот плывет со скоростью течения реки , следовательно:
30 : 5 = 6 ч . - время , которое он затратил
6-1 = 5 ч. - затратила лодка на путь туда-обратно
Лодка:
Собственная скорость - х км/ч
По течению:
Скорость - (х+5) км/ч
Расстояние - 60 км
Время - 60 /(х+5) ч.
Против течения :
Скорость - (х-5) км/ч
Расстояние - 60 км
Время - 60/(х-5) ч.
Уравнение.
60/(х+5) + 60/(х-5) = 5
(60(х-5) +60(х+5) ) / (х²-25) = 5 * (х²-25)
60х - 300 +60х +300 = 5(х²-25)
120 х = 5х²-125
120х -5х² + 125 =0 ÷(- 5)
х²-24х- 25=0
D= (-24)² - 4 *(-25) = 576+100=676
D > 0 - два корня
х₁= (24-√676) /2 = (24-26)/2 = -2/2=-1 - не удовл. условию задачи
х₂= (24+26 )/2= 50/2 =25 - собственная скорость лодки
т.к. 6>0, то равносильно двум неравенствам:
|||x|+9|+1|-5>6 и |||x|+9|+1|-5<-6
|||x|+9|+1|>11 и |||x|+9|+1|<-1
т.к. -1<0, а значение модуля не может быть отрицательным числом, то нер-во |||x|+9|+1|<-1 не имеет решения. продолжаем решать |||x|+9|+1|>11:
т.к. 11>0, то равносильно двум неравенствам:
||x|+9|+1>11 и ||x|+9|+1<-11
||x|+9|>10 и ||x|+9|<-12
т.к. -12<0, а значение модуля не может быть отрицательным числом, то нер-во
||x|+9|<-12 не имеет решения.
||x|+9|>10
т.к. 10>0, то равносильно двум неравенствам:
|x|+9>10 и |x|+9<-10
|x|>1 и |x|<-19 (не имеет решения)
|x|>1
равносильно двум неравентсвам:
x>1 и x<-1
ответ x∈(-∞;-1)V(1;+∞)