См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
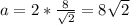 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
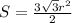 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

1.
Приравниваем обе части
х-1=-х+3
2х=3+1=4
х=2
Подставляем в 1-ре уравнение
у=2-1=1
ответ: (2,1)
2.
Выразим 4а из 1-ого уравнения
4а=2+6b
Подставляем во 2-ое
2+6b+2b=3
8b=1
b=1/8
Ищем а:
2а-3*(1/8)=1
2a=1+3/8=11/8
a=11/16
ответ (11/16,1/8)
4.
Пусть х - количество монет номиналом по 2 рубля, а у количество монет носиком по 5 рублей
Составляем систему:
х+у=18
2х+5у=97
Из 1-ого вырадаем х:
х=18-у
Подставляем во 2-ое
2(18-у)+5у=97
36-2у+5у=97
3у=97-36=61
у=61/3
х=18-61/3=-7/3
Объяснение:
Кажется в 4 номере неправильные цифры, т. к. получилось, что количество монет, дробное или отрицательное число
1)
х - большее число
у - меньшее число
ху -18 = 2х
х + у = 11
Из второго выражаем у через х
у = 11 - х
Подставляем это значение в первое уравнение
х(11-х) - 18 = 2х
-х*х + 9х - 18 = 0
х1 = 6 у1 = 5
х2 = 3 у2 = 8
Так как у < х, единственный правильный вариант - эти числа 5 и 6.
2)
х - количество двухместных лодок
у - количество трёхместных лодок
2х - сколько человек помещаются в двухместные лодки
3у - сколько человек помещаются в трёхместные лодки
2х + 3у = 14
х + у = 6
Выразим из второго уравнения у через х
у = 6 - х
Подставляем это значение в первое уравнение^
2(6-у) + 3у = 14
12 - 2у + 3у = 14
12 + у = 14
у = 2
Значит у причала стояло 2 трёхместных и 4 двухместных лодки.