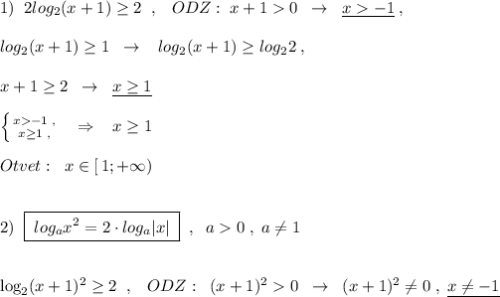
![2\, log_2|x+1|\geq 2\; \; \to \; \; \; log_2|x+1|\geq 1\; \; ,\; \; log_{2}|x+1|\geq log_22\; ,\\\\|x+1|\geq 2\; \; \to \; \; \; \left [ {{x+1\geq 2} \atop {x+1\leq -2}} \right.\; \; \left [ {{x\geq 1} \atop {x\leq -3}} \right.\; \; \Rightarrow \\\\Otvet:\; \; x\in (-\infty ,-3\, ]\cup [\, 1,+\infty )](/tpl/images/0838/6182/898bc.png)
P.S. Свойство 
верно только для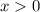 
. Но под знаком log в его аргументе может стоять квадрат какого-то выражения, т.к. квадрат любого выражения неотрицателен (больше или равен 0) . Из-за области определения логарифмической функции мы требуем , чтобы аргумент был строго больше 0, то есть остаётся, чтобы квадрат выражения не равнялся 0 . Во 2 (чётную) степень может возводится не только положительное, но и отрицательное выражение 
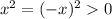, а под знаком log должно остаться строго положительное выражение, поэтому в общем случае в аргументе log , надо писать модуль аргумента. Поэтому в общем случае действует свойство log , обведённое в рамочку.
Объяснение:
ответ: y=-1.