Объяснение:
Александр упаковал 400 больших коробок и израсходовал два рулона скотча полностью, а от третьего осталось ровно две пятых,то есть:
2+(1-(2/5))=2+(3/5)=2³/₅ (рулона).
65 см=0,65 м 55 см=0,55 м.
Найдём количество метров в одном рулоне:
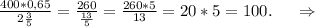
Количество метров в трёх рулонах скотча: 100*3=300. ⇒
Если на каждую коробку нужно по 0, 55 м скотча, то на 560 одинаковых коробок ему нужно:
560*0,55=308 (м) ⇒
ответ: трёх целых таких рулонов скотча ему не хватит.
Первая труба наполнит бассейн за: T1 час;
2. Второй трубой бассейн наполнится за: T2 час;
3. Скорость наполнения первой трубы: P1 = 1/T1 (1/час);
4. Скорость наполнения второй трубы: P2 = 1/T2 (1/час);
5. Составляем два уравнения по условиям задачи:
0,1 * (1 / P1) + 0,9 * (1 / P2) = 4;
0,9 * (1 / P1) + 0,1 * (1 / P2) = 28/3;
6. Заменяем переменные:
0,1 * T1 + 0,9 * T2 = 4;
0,9 * T1 + 0,1 * T2 = 28/3;
T2 = (4 - 0,1 * T1) / 0,9;
0,9 * T1 + 0,1 * (4 - 0,1 * T1) / 0,9 = 28/3
8,1 * T1 + 4 - 0,1 T1 = 84;
8 * T1 = 80;
T1 = 80 / 8 = 10 часов.
ответ: первая труба наполнит бассейн за 10 часов
Необходимо доказать тождество:
cos4a + 1 = ½ sin4a (ctg a - tg a)
Доказательство:
Из формулы понижения степени имеем:
cos^2(2a) = (1+ cos(4a) ) / 2
Таким образом:
cos4a + 1 = 2cos^2(2a) = 2cos(2a) * sin(2a) *cos(2a)/sin(2a) =
= sin(4a) * cos(2a)/sin(2a) = sin(4a) * (cos^2(a) - sin^2(a) ) / (2cos(a) * sin(a) ) =
= ½ sin4a * (cos^2(a) - sin^2(a) ) /(cos(a) * sin(a)) =
= ½ sin4a (cos(a)/sin(a) - sin(a)/cos(a) ) = ½ sin4a (ctg a - tg a)
Применяются формулы:
sin(2x) = 2sin(x)*cos(x)
сos(2x) = cos^2(x) - sin^2(x)
Что и требовалось доказать