Вниз по реке-это значит, что течение плыть катеру, т.е. полная скорость катера за в это путешествие составляло х+21 км/ч, где х-скорость течения реки. Получается обратно скорость катера была меньше, т.к. течение уже мешало плыть катеру, т.е. обратно скорость катера составляла: 21-х км/ч. Пусть у - это время всего путешествия катера - туда и обратно. Составим уравнение относительно скорости реки "х" и решим его: Путешествие катера из города А в город В: (х+21)m=72 (x-21)n=72 m+n=y Здесь: m-время пути катера из города А в город В, а n-время пути катера обратно, тогда: m=y-n
(х+21)(y-n)=72 (x-21)n=72
Время пути канистры: х*у=21
Получаем систему уравнений:
(х+21)(y-n)=72 (x-21)n=72 х*у=21
x*y-x*n+21*y-21*n=72 x*n-21*n=72 х*у=21
21-x*n+21*y-21*n=72 x*n-21*n=72 х*у=21
21-x*n+21*y-21*n=72 n(x-21)=72 х*у=21
21-21n+72-21n+21y=72 n(21/y - 21)=72
-42n+21y=-21 :21 n=72/(21/y - 21)
-2n+y=-1 n=72/(21/y - 21)
y=2n-1 n*(21/(2n-1) - 21)=72 n*(21-42n+21)=72(2n-1) -42n²+42n-144n+72=0 -42n²-102n+72=0 -21n²-51n+36=2601+12096=5625 √5625=75 n1=(51+75)/-42=-3 <0 - ответом быть не может (скорость не может быть отрицательной) n2=(51-75)/-42=24/42=12/21
Ну начнем с самого неприятного и сложного: cos^2(3a/2-pi/8) тут применим понижение степени: (1+cos(3a-pi/4))/2 далее проделаем такую хитрость: cos(3a-pi/4)=cos(3*a -3*pi/4-pi/4 +3pi/4)=cos(3(a-pi/4)+pi/2)=-sin(3(a-pi/4)=sin(3*(pi/4-a))=3*sin(pi/4-a)- 4*sin^3(pi/4-a)=3*1/3 -4*1/27=1-4/27=23/27 (1+cos(3a-pi/4))/2=(1+23/27)/2=25/27 Теперь вспомним что: √2 * sin(pi/4-a)=(cos(a)-sin(a))=√2/3 (вытекает из формулы синуса разности. И тут довольно элегантно находиться : (cosa-sina)^2=cos^2+sin^2a-sin2a. sin2a=1-(cosa-sina)^2=1-2/9=7/9 cos4a=1-2sin^2(2a)=1-98/81=-17/81. Осталось посчитать: 6*(7/9-17/81)-8*(25/27)=6*(46/81)-8*(75/81)=(6*46-8*75)/81=-324/81=-4 ответ: -4. Но мне почему то кажется, что я сделал не самым простым
Методом подбора корней получается один корень: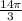
Неравенство вроде простое, но я не пойму условие: ^-это квадрат или что?