№ 1. (8 4/5 - 13,8 : 3 5/6) · 12/13 = 4 целых 4/5 = 4,8.
1) 13,8 : 3 5/6 = 138/10 : 23/6 = 69/5 · 6/23 = (3·6)/(5·1) = 18/5 = 3 3/5
2) 8 4/5 - 3 3/5 = 5 1/5 = 26/5
3) 26/5 · 12/13 = (2·12)/(5·1) = 24/5 = 4 4/5 = 4,8
№ 2. 1 - 0,15 : (11/12 - 0,75) = 0,1.
1) 11/12 - 0,75 = 11/12 - 3/4 = 11/12 - 9/12 = 2/12 = 1/6
2) 0,15 : 1/6 = 3/20 · 6/1 = (3·3)/(10·1) = 9/10 = 0,9
3) 1 - 0,9 = 0,1
№ 3. 8,3 - (3 5/12 - 1 1/3) : 5/12 = 3,3.
1) 3 5/12 - 1 1/3 = 3 5/12 - 1 4/12 = 2 1/12 = 25/12
2) 25/12 : 5/12 = 25/12 · 12/5 = 25/5 = 5
3) 8,3 - 5 = 3,3
x^2-6x+19=0
a=1 b=-6 c=19
D=b^2-4ac=(-6)^2-4*1*19=36-76<0, следовательно, решений нет. ответ: решений нет.
x^2-6x+9=0
a=1 b=-6 c=9
D=b^2-4ac=(-6)^2-4*1*9=36-36=0, следовательно, ур-е имеет единственный корень, который мы можем вычислить по формуле: x=(-b)/2a=-(-6)/2*1=6/2=3 ответ: 3.
x^2-6x=0
Вынесем "х" за скобку:
x(x-6)=0
Произведение равно 0 тогда, когда хотя бы один из множителей равен 0. Следовательно:
x=0 или x-6=0 x=6 ответ: 0, 6.
x^2-6=0
x^2=6
Извлекаем квадратный корень из двух частей и получаем:
![x=\sqrt[2]{6} \\x=-\sqrt[2]{6}](/tpl/images/4424/0353/fa5da.png)
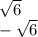
я не понимаю