
ДАНО
Y=(x²-4)/(x²+1)
ИССЛЕДОВАНИЕ
1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. x = 0. В числителе - (x² - 4) = (x-2)*(x +2) = 0
x1 = -2, x2 = 2
3. Пересечение с осью У. У(0) = -4.
4. Поведение на бесконечности.
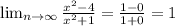
Горизонтальная асимптота - Y = 1.
5. Исследование на чётность.Y(-x) = Y(x). Функция чётная.
6. Производная функции.
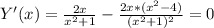
7. Локальные экстремумы.
Максимума - нет, минимум – Ymin(0) = -4.
8. Интервалы монотонности.
Убывает - Х∈(-∞;0]. Возрастает - Х∈[0;+∞)
9. Вторая производная - Y"(x).
Корни производной - точки перегиба: х1 =-√3/3, х3=√3/3. (≈0.58)
9. Выпуклая “горка» Х∈(-∞;-√3/3)∪(√3/3;+∞),
Вогнутая – «ложка» Х∈(-√3/3;√3/3).
10. Область значений Е(у) У∈(-4;1)
11. График в приложении
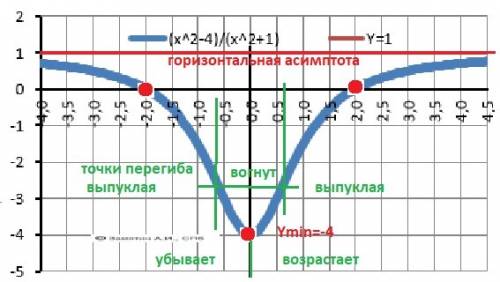
Объяснение:
При сдвиге вдоль оси OX вправо из х вычитается величина сдвига, при сдвиге влево к х прибавляется величина сдвига.
При сдвиге вверх вдоль оси OY к правой части уравнения прибавляется величина сдвига, при сдвиге вниз вычитается величина сдвига.
1) Вдоль оси OX сдвинули влево на 2, вдоль оси OY вверх на 3. Итого получаем уравнение:
у = 3(х + 2)² + 3
Аналогично решаем:
2) у = -3(х + 1)² - 3
3) у = (х - 2)² + 3
4) у = -5(х - 3)² - 1