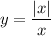
Как раскрывается модуль? 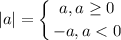
То есть при a>0 знак не меняем, при а=0 все равно, ноль хоть с плюсом, хоть с минусом равен 0, а если число отрицательное, то с минусом.
Здесь так же.
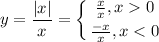
Почему х не может быть равен 0? Потому что он в знаменателе, а на остальной части числовой прямой он определен.
Преобразуем:
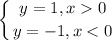
то есть при x>0 мы строим прямую y=1, а при x<0 строим прямую y=1.
Надо понимать, что прямая y=1 при х=0 дает точку (0;1), но раз x≠0, то точка (0;1) должна быть выколотой (её там не существует на самом деле, так обозначают, это разрыв функции)
Аналогично с x<0, там строим прямую y=-1 и точку (0;-1) так же выкалываем. Всё, как нарисовано на рисунке в тетради.
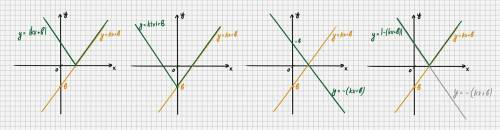
a) Сначала строиться эскиз прямой y = kx + b, затем, всё что ниже оси OX симметрично относительно неё [оси] переносится наверх. Получается галочка.
*Модуль все отрицательные значения функции делает положительными, в результате такого преобразования "отрицательная" часть прямой станет положительной (пр. значения -2; -4; -18 перейдут в значения |-2|; |-4|; |-18| или 2; 4; 18)
б) Строиться эскиз прямой y = kx + b, после правая часть графика (при x > 0) остаётся неизменная, а левая часть строиться симметрично относительно оси OY. Тоже получится галочка.
*Модуль над неизвестной при x < 0 будет преобразовывать его в положительный, тем самым при подстановке будут получаться одинаковые значения (y) при противоположных значениях x.
в) Строиться эскиз прямой y = kx + b, а потом получившуюся прямую (всю) отражают симметрично относительно оси OX. Тем самым все значения прямой-эскиза станут противоположными (пр. 2 ⇒ -2; -5 ⇒ 5)
г) Выполняются все шаги пункта в), затем шаг из пункта а).
*По факту модуль над всем выражением уберёт знак "-" перед kx + b, тем самым получится прямая из пункта а), поэтому можно сразу переходить к нему, не выполняя пункт в)
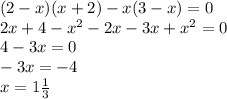
ответ: 1 1/3