Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz, задана прямая a и точка формула, не лежащая на прямой a. Поставим перед собой задачу: получить уравнение плоскости формула, проходящей через прямую a и точку М3.
Сначала покажем, что существует единственная плоскость, уравнение которой нам требуется составить.
Напомним две аксиомы:
через три различные точки пространства, не лежащие на одной прямой, проходит единственная плоскость;
если две различные точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Объяснение:
В решении.
Объяснение:
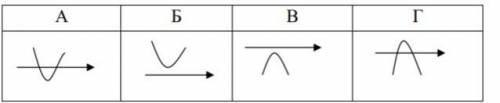
Дискримінант квадратного рівняння ax² + bx + с = 0 дорівнює -1, a = 2. Укажіть вигляд графіка відповідної квадратичної функції.
Дискриминант уравнения = -1, то есть, < 0.
Уравнение в этом случае не имеет корней, а парабола не пересекает ось Ох.
Коэффициент а = 2, значит, ветви параболы направлены вверх.
Этим двум условиям соответствует график под Б.