
Объяснение:
так, рассмотрим этот пример:
Пример 3, упростить выражение:
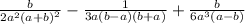
здесь, автор пытался донести, что нам нужно домножить на определенные числа, дабы получить общий знаменатель 6а³(а-b)(a+b)²
При этом, он имел ввиду, что умножение на второй знаменатель можно произвести по разному:
1) если использовать общий множитель
6а³(b-a)(a+b)² , то домножить нужно на 2а²(а+b), и это действительно не принципиально, но тогда третий множитель будет "страдать" - нужно будет домножить его уже со знаком "-": -(a+b)², чтобы при умножении, как вы и сказали: (а-b) = -(b-a) и при умножении двух минусов, мы получаем знак "+"
, так и наоборот для второго случая:
2)если использовать общий множитель
6а³(а-b)(a+b)² , то домножить второй знаменатель нужно на -2а²(а+b)!
А третий на (a+b)², с плюсовым перед стоящим знаком.
И не забываем так же про первый знаменатель :)
Тут всё дело в том, какой общий множитель вы захотите использовать.
Надеюсь, понятно объяснил.
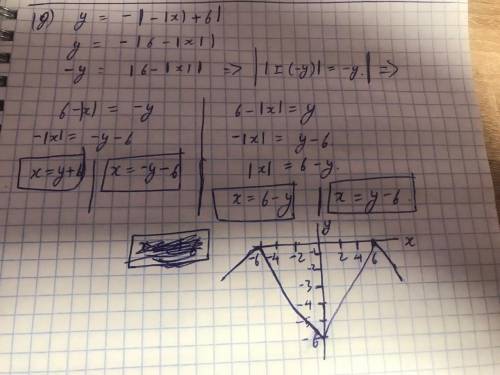
Строим график по шагам.
Объяснение:
Шаг 1:
Строим график функции у=|Х|
Весь график находится над ОХ
(графиком являются биссектри-
сы 1 и 2 координатных четвертей).
Шаг 2:
Строим график функции
У= -|Х|
Для этого зеркально (то есть сим
метрично оси ОХ) отражаем уже
построенный график функции
У=|Х|
Весь график расположен под
осью ОХ.
Шаг 3:
Строим график функции У= -|Х|+6
Для этого график функции У= -|Х|
перемещае вдоль оси ОУ вверх
на 6 единиц (совершаем парал
лельный перенос вдоль положи
тельного направления оси ОУ
на 6 единичных отрезков).
Шаг 4:
Строим график функции
У=|-|Х|+6|
Как это сделать?
Модуль не может быть отрица-
тельным, поэтому возвращаемся
к графику функции У= -|Х|+6 и
все, что находится под осью ОХ
отражаем симметрично относи
тельно этой оси в верхнюю по
луплоскось (зеркальное отра
жение). Весь график располо
жен НАД осью ОХ.
Шаг 5:
Строим график искомой функции:
Для этого график, построенный
на 4 шаге, симметрично отража
ем в нижнюю полуплоскость. (Зер
кальное отражение относитель
но оси абсцисс).
Весь график расположен ПОД
осью ОХ.
Объяснение:
ctg A. 1
+ - 9
tg A. sin A
точных формул не помню, это вроде тригонометрия, если не ошибаюсь