Пусть скорость первого самалета х км/час, второго- х-100 км/час.
1800/(х-100)-1800/х=0,6
1800х-1800х+180000-0,6х^2+60x=0
0.6x^2-60x+180000=0
D=3600+432000=435600
d=660
x1=60+660/1.2=600
x2=60-660/1.2=-500
Условия задачи удовлетвояет только х1=600 , так как скорость не может быть отрицательной.
Скорость первого самелета 600 км/час, второго - 500 км/час.
решите систему уравнений методом подстановки общая скобка один пример сверху другой снизу 3x-y=-5. -5x+2y=1, т. е из одного уравнения выразить одну переменную и подставить во второе. Из двух уравнений проще выразить из первого у, т. к. коэффициент равен 1, получим
3x-y=-5
-5x+2y=1
Выражаем у из первого уравнения и ставим во второе
у=3х+5
-5х+2(3х+5)=1
Раскрываем скобки
у=3х+5
-5х+6х+10=1
Приводим подобные
у=3х+5
х+10=1
Отсюда
у=3(-9)+5
х=1-10
Или решением неравенства будет пара
у=-22
х=-9
Проверка
3(-9)-(-22)=-5
-5(-9)+2(-22)=1
Произведем вычисления
-27+22=-5
45-44=1
или
5=-5
1=1
Т. к. получили верное равенство, значит, решили правильно
ответ: х=-9 и у=-22 или (-9;-22)
Удачи!
Объяснение:
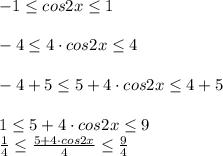
![[ \frac{1}{4};2 \frac{1}{4}]](/tpl/images/0413/8761/f42ca.png)
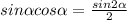
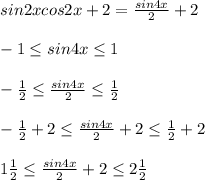
![[1 \frac{1}{2};2 \frac{1}{2}]](/tpl/images/0413/8761/944ce.png)
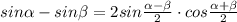
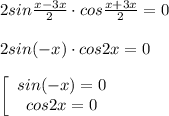
x - скорость первого самолета
х-100 - скорость 2-го самолета
1800 /х - время в пути 1-го
1800 / (х-100) - время в пути второго
1800/(х-100) - 1800/х = 36/60
1800х - 1800х + 180000 = (36/60)*х*(х-100)
180000=0,6*х² - 60х
0,6х²-60х-180000=0
х²-100х-300000=0
х1=600км х2=-500км
Скорость первого 600 км/час
Скорость второго 500 км/час