с³-27а³
с³-3³а³
с³-(3а)³
(с-3а)*(с²+с*3а+(3а)²)
(с-3а)*(с²+3ас+9а²)
2. Пусть х-1-ый день
х-5 - км 2-ой день
3 день
3/7 * (х+х-5)
всего х+х-5 + 3/7 * (2 х-5) = 110
14 х-35+6 х-15=770
20 х=720
х=36 - 1 день
36-5=31 - 2 день
110-36-31=43 - 3 день
1. Принимаем за х расстояние, которое пешеход до встречи.
(17 - х) км проехал велосипедист до встречи.
2. 15 минут = 15/60 часа = 0,25 часа.
3. Составляем уравнение и решаем его:
х/4 - (17 - х)/12 = 0,25;
(12х - 68 + 4х)/48 = 0,25;
16х = 80;
х = 5.
Велосипедист проехал от города до места встречи 17 - 5 = 12 км.
ответ: пешеход до места встречи 5 километров, велосипедист проехал 12 километров.
Объяснение:
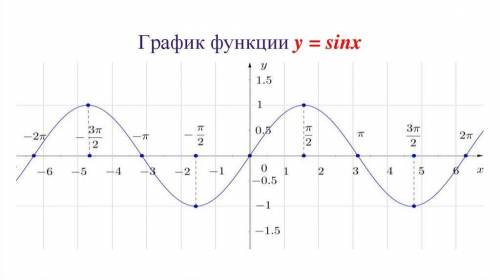
у = sin(x)
Область определения: D(f) = (-∞; +∞) или D(f)∈RОбласть значения: E(f) = [-1; 1]Нули функций: x₀ = πn, n∈ZЧетность функций: sin(-x) = -sin(x) - нечетнаяПериод функций: sin(x+T) = sin(x) ⇒ T = 2πПромежутки монотонности:y = sin(x)↑ на [-π/2 + 2πn; π/2 + 2πn], n∈Z
y = sin(x)↓ на [π/2 + 2πn; 3π/2 + 2πn], n∈Z
Промежутки знакомо постоянства:y>0 при x∈(0 + 2πn; π + 2πn), n∈Z
y<0 при x∈(π + 2πn; 2π + 2πn), n∈Z
Наибольшее и наименьшее:y = 1 - наибольшее при x = π/2 + 2πn,n∈Z;
y = -1 - наименьшее при x = − π/2 + 2πn,n∈Z;
Обратимость: y = arcsin(x) на [- π/2; π/2]Ограниченность: Ограничена сверху и снизуПроизводная: y = (sin(x))' = cos(x)График: (показано внизу)↓